
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Diagonalisation | Triangulation | Exercices |
Cette page suppose connues les notions d'application linéaire, de matrice d'application linéaire, de déterminant, de valeur propre et de vecteur propre :
➔ La résolution de systèmes d'équations linéaires algébriques ou différentiels, l'étude de suites récurrentes et d'une façon générale tout sujet d'étude se résumant à une équation du type AX = B, peut être grandement facilité si l'on peut exprimer le problème dans une base (changement de coordonnées) où la matrice A du système considéré prend une expression simplifiée : le plus possible de zéros.
Soit E un espace vectoriel de dimension n sur le corps K = R ou C (nombres réels ou complexes). On note B = (e1, e2, ..., en) et B' = (e'1, e'2, ..., e'n) deux bases de E.
Il s'agit, connaissant les coordonnées x1, x2, ..., xn d'un vecteur u relativement à B, d'exprimer ses coordonnées x'1, x'2, ..., x'n relativement à B' et inversement. Chaque vecteur e'j s'exprime de façon unique dans la base B sous la forme :
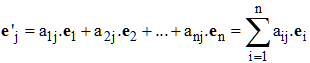
On a alors :
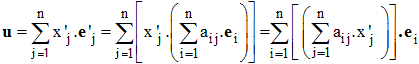
On identifie cette dernière égalité à :
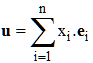
Ce qui fournit, selon la multiplication d'une matrice par un vecteur colonne :
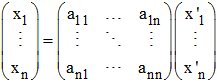
La matrice :
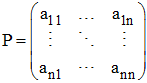
est appelée matrice de passage de B à B'.
! Cette appellation est regrettable car elle devrait exprimer le contraire puisqu'on exprime ci-dessus les anciennes coordonnées en fonction des nouvelles : on obtient les anciennes coordonnées xi de u dans la base B en fonction des nouvelles coordonnées x'i dans la base B'. La matrice P est inversible puisque ses colonnes représentent les vecteurs de la base B' écrits dans la base B. Avec la notation matricielle, on a donc :
Exemple : Lorsque dim E = 2; si B = (i,j) et B' = (u,v) avec u = i + 3j et v = -2i + j, on a :

Pour un vecteur X = x.i + y.j = x'.u + y'.v, on aura :

D'où, x = x' - 2y' , y = 3x' + y' et, inversement : x' = (x + 2y)/7 , y' = (-3x + y)/7
➔ Lorsque P est orthogonale, le calcul de P-1 s'en trouve grandement facilité : dans ces condition P-1 = tP (transposée de P) :
Calcul pratique d'une matrice inverse : » » Hermite
| Matrices semblables : |
Si f est un endomorphisme d'un espace vectoriel E de dimension n sur le corps K = R ou C, notons M/B sa matrice relativement à B = (e1, e2, ..., en) et si X/B = (x1, x2, ..., xn), posons Y = f(X). En passant à la base B' = (e'1, e'2, ..., e'n), on peut écrire sous forme matricielle, en notant P la matrice de passage :
X/B = P![]() X/B'
, Y/B = P
X/B'
, Y/B = P![]() Y/B' , Y = M/B
Y/B' , Y = M/B![]() X. Par suite : PYB' =
(M/B
x P)
X. Par suite : PYB' =
(M/B
x P)![]() X/B' et en multipliant par P-1
: YB' =
(P-1 x
M/B
x P)
X/B' et en multipliant par P-1
: YB' =
(P-1 x
M/B
x P)![]() X/B' . Ce qui montre que la matrice de f,
relativement à B', est :
X/B' . Ce qui montre que la matrice de f,
relativement à B', est :
On dit que les matrices M/B' et M/B sont semblables. D'une façon générale, deux matrices M et N sont dites semblables s'il existe une matrice inversible P telle que N = P-1 x M x P.
∗∗∗
Vérifier que la relation "est semblable à " est une
relation
d'équivalence dans
l'ensemble Mn
des matrices carrées d'ordre n.
Trace d'une matrice et d'un endomorphisme :
On appelle ainsi la somme des éléments diagonaux d'une matrice et on note Tr(A) = Σaii la trace de la matrice A = (aij). La trace jouit de remarquables propriétés algébriques.
C'est une forme linéaire : Tr(A + B) = Tr(A) + Tr(B) et Tr(αA) = αTr(A).
La trace est invariante par transposition
: Tr(tA) = Tr(A).
En particulier si A est orthogonale, Tr(A-1)
= Tr(A).
Tr(A × B) = Tr(A) × Tr(B).
Deux matrices semblables ont même trace : Tr(P-1 × A × P) = Tr(A × P-1 × P) = Tr(A × I) = Tr(A).
Preuve du point 3 : notons pij = Σk(aikbkj), Σk désignant une somme par rapport à k, et qij = Σk(bikakj) les termes généraux des matrices A × B et B × A. Tr(A × B) = Σipii = Σi(Σkaikbki). Mais on peut intervertir l'ordre de sommation Σpii = Σk (Σiaikbki) = Σk(Σibkiaik) = Σkqkk = Tr(B × A).
Le résultat 4 permet de définir la trace d'un endomorphisme φ de E : c'est la trace de la matrice de φ dans une base quelconque de E (indépendance par rapport à la base utilisée). On a alors en particulier :
|
Matrice diagonale : |
On dit qu'une matrice A = (aij) est diagonale pour exprimer que les seuls éléments non nuls de A sont ceux de même rang en ligne et en colonne, à savoir les aii (pour tout i ≠ j, aij = 0). Si, par un changement de base, une matrice s'avère diagonale, on dit qu'elle a été diagonalisée.
Théorème :
Lorsque E est de dimension finie n, si f est un endomorphisme admettant n valeurs propres distinctes, de vecteurs propres associés v1, v2, ..., vn , alors ceux-ci constituent une base de E et relativement à cette base (v1, v2, ..., vn) la matrice de f prend la forme diagonale :

Remarques :
Mais qu'en est-il lorsque f possède des valeurs propres multiples ? la diagonalisation est possible dans certains cas :
Théorème 1 :
Théorème 2 :
Toute matrice symétrique (c'est à dire lorsque aij = aji pour tout i et j) est diagonalisable au moyen d'une matrice de passage orthogonale (les vecteurs-colonnes constituent une base orthonormée, » Hermite).
∗∗∗
Exercice 2 sur cette page ,
Étude d'une matrice de Markov
|
Matrice triangulaire (ou matrice trigonale) : |
Si une matrice n'est pas diagonalisable, on peut chercher à obtenir une matrice triangulaire, c'est à dire une matrice de la forme :
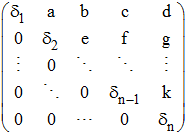
ce qui est toujours possible lorsque K = C. On parle de matrice triangulable (ou trigonalisable) et de triangulation. La matrice ci-dessus est, plus précisément triangulaire supérieure, car les éléments éventuellement non nuls sont situés au-dessus des éléments diagonaux δ1, δ2, ..., δn. Dans le cas contraire, on parle de matrice triangulaire inférieure.
Réduite de Gauss : »
➔ Indépendamment de tout endomorphisme, on peut manipuler une matrice en tant qu'opérateur sur des vecteurs colonnes, Par exemple, si on écrit, relativement à une base B = (i,j) :

cela signifie que M × i = 2i + j et M × j = i - j :
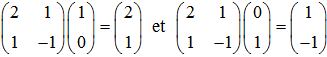 » matrice
colonne
» matrice
colonne Théorème de Jordan :
Lorsque K = C, toute matrice carrée peut se mettre, au moyen d'un changement de base approprié, sous la forme :

où les blocs Δ1, Δ2, ... Δn sont des matrices carrées dont les termes δi,i de la diagonale principale sont égaux, les autres termes étant nuls à l'exception de δi,i+1 = 1 (blocs de Jordan). Si K = R, cette forme peut être obtenue pour une matrice n x n par recherche de ses valeurs propres si celle-ci admet n valeurs propres éventuellement multiples.
On parle de diagonalisation par blocs ou, parfois, de jordanisation d'une matrice, fort utile dans la résolution d'équations différentielles linéaires ainsi que dans celle de systèmes de suites récurrentes linéaires.
➔ Pour plus de théorie, on pourra consulter le lien proposé en fin de page consacrée à Jordan
∗∗∗
Systèmes
différentiels linéaires :
d'ordre
2 (valeurs propres réelles) ,
d'ordre
3 (valeurs propres complexes)
∗∗∗
1.
E est de dimension 2 sur R; B = (i,j) est une
base de E; f est l'endomorphisme dont la matrice relativement
à B est :
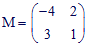
 (matrice de changement de
base)
(matrice de changement de
base)
∗∗∗
2.
On considère la matrice :
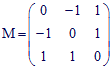
Ses colonnes s'identifient à la matrice d'un endomorphisme f d'un espace vectoriel réel E de dimension 3, relativement à une base B = (i, j, k)

et vérifier ce résultat en appliquant la formule de changement de base M' = P-1MP où P est la matrice de passage de B à B' en calculant au préalable la matrice inverse P-1.➔ on voit donc, sur cet exemple, qu'une matrice dont les valeurs propres sont multiples peut être diagonalisée. Mais ce n'est pas toujours possible.
Réduction d'une forme quadratique : »
∗∗∗
3.
E est de dimension 3 sur R; B = (i,j,k) est une
base de E; relativement à B une matrice M s'écrit
:


4i/ M/B' est triangulaire inférieure. On pose w = a.u + b.v + c.k où a, b et c sont réels et c ≠ 0. Montrer que l'on peut trouver a, b et c afin d'obtenir, relativement à B" = (u, v, w) :

Rép. : On écrit que M/B'w, doit être de la forme α.u + β.v + γ.w = (α + γa).u + (β + γb).v + γc.k) ce qui conduit au système :
2a - 2c = α + γa ; 4b - 3c = β + γb ; 4c = γc. On a donc γ = 4 car c est non nul, b s'élimine et le système se réduit à α = -2(a + c), β = -3c.
Il est alors loisible de choisir b = 0; c = -1/3, a = -c. On a alors finalement a = 1/3, b = 0, c = -1/3, α = 0, β = 1, γ = 4.
D'où w(1/3,0,-1/3) relativement à B = (i,j,k) et relativement à cette base B"= (u, v, w), la 3è colonne de M est [α , β , γ ] = [0, 1, 4].
4.
Soit M une matrice réelle 3 ×
3
telle que M2 non nulle mais M3 nulle. Montrer que M
est triangulable.
»
par hypothèse,
il existe u non nul tel que M2u ≠ 0. Montrer
que (u,Mu,M2u) est une base de R3...
∗∗∗
5.
On se propose de trianguler la matrice M ci-dessous écrite
dans une B = (i,j,k) de E.
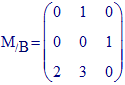
i/ Dans quelle base simple M est-elle triangulaire ?
Au vu de la matrice M, si la ligne 3 "passe" en première ligne, c'est à dire si l'on passe de la base B = (i,j,k) à la base B' = (k,i,j), la matrice relativement à B' est triangulaire (inférieure) :
➔ M/B et M/B' ne sont pas semblables, au sens de l'algèbre des matrices. On constate d'ailleurs que la trace de M/B' égale 4 alors que celle de M/B est nulle (deux matrices semblables ont même trace).
ii/ Calculer les valeurs propres de la matrice M/B en calculant les racines (valeurs propres) de son polynôme caractéristique .
Rép. : det(M - λI) = -(λ3 - 3λ - 2); λ1 = -1 (double) et λ2 = 2.iii/ Montrer que l'on peut choisir u = -i + j - k, v = i + 2j + 4k, w = j comme base de E où u et v sont des vecteurs propres de M, et que si P est la matrice de passage relative à cette base, on a :
» On voit, là encore (cf. exo3) que la réduction d'une matrice à la forme triangulaire n'est pas unique. Elle dépend de la base choisie. Lorsqu'il est possible de jouer sur des permutations de lignes (ce qui revient à permuter les vecteurs de base correspondants), il ne faut pas hésiter à moins que des contraintes liées au sujet traité n'interdise cet artifice.