
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» cas 3 × 3 et matrice inversible |
(a,b,c) désignant un triplet de R3, on considère le système (s) d'équations linéaires d'inconnues réelles x, y, z, t :

1°/ Sans calculer le déterminant du système, constater en procédant par triangulation (méthode du pivot) que le système (s1) ci-dessous, dans le cas a = b = c = 1, admet une unique solution que l'on précisera :

2°/ Constater en procédant par triangulation (méthode du pivot) que le système (s2) ci-dessous, dans le cas a = 1, b = 2, c = -1, n'admet aucune solution :

3°/ On note A la matrice 4 x 4 associée au système (s) :
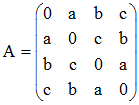
Le système (s) peut alors s'écrire :

a/ Calculer le déterminant D de la matrice A et le factoriser. Utiliser D afin de retrouver le résultat de 2°/ selon lequel le système (s2) admet une unique solution.
b/ Vérifier, en les combinant, que les équations de (s2) sont incompatibles.
4°/ Reprendre la résolution du système (s1) par calcul de la matrice A-1.
Si vous séchez après avoir bien cherché : ››››
| Solution : |
1°/ Ecrivons le tableau des coefficients du système (s1) où les 4 premières colonnes représentant sa matrice (aij) :

Le premier pivot a11 est nul : on échange les lignes 1 et 2 :

Le premier pivot est désormais 1 et on a ainsi 0 en a21. On procède à l'apparition d'un zéro en a31 en remplaçant L3 par L3 - L1 et pour un zéro en a41, on remplace L4 par L4 - L1 :

Le second pivot est a22 = 1. Il nous faut faire apparaitre des zéros sous ce pivot en ligne 3 et 4. On remplace L3 par L3 - L2 et L4 par L4 - L2 :

Le troisième pivot est maintenant a33 = -2. Il nous faut faire apparaitre un zéro sous ce pivot en ligne 4. On remplace L4 par L4 - L3/2 :

La dernière ligne de notre système équivaut à -3t/2 = -1/2, soit t = 1/3. La ligne 3 fournit ensuite = -2/3, la ligne 2 conduit à y = 4/3 et la ligne 1 à x = -2/3. La solution est unique :
(x, y, z, t) = (-2/3, 4/3, -2/3, 1/3)
2°/ Comme précédemment, écrivons le tableau des coefficients du système (s2) :

Le premier pivot a11 est nul : on échange les lignes 1 et 2 :

On a 0 en a21. On procède à l'apparition d'un zéro en a31 en multipliant L1 par 2 et en remplaçant L3 par L3 - 2L1 et pour un zéro en a41, on remplace L4 par L4 +L1 :

Le second pivot est a22 = 1. Il nous faut faire apparaitre des zéros sous ce pivot en ligne 3 et 4. On remplace L3 par L3 + L2 et L4 par L4 - 2L2 :

Le troisième pivot est a33 = 4. Il nous faut faire apparaitre un zéro sous ce pivot en ligne 4. On remplace L4 par L4 + L3 :

 Petit
souci... Le 4ème pivot est nul ! Cela signifie que le système est singulier :
son déterminant est nul. La ligne 4 conduit à 0t = 1, soit 0 = 1 : aucune
solution.
Petit
souci... Le 4ème pivot est nul ! Cela signifie que le système est singulier :
son déterminant est nul. La ligne 4 conduit à 0t = 1, soit 0 = 1 : aucune
solution.
3°/ a) Le développement selon la 1ère colonne fournit :

On développe facilement les déterminants d'ordre 3 : D = a4 + b4 + c4 - 2a2b2 - 2b2c2 - 2a2c2 et on reconnaît non moins facilement la présence d'un carré... :
D = (a2 - b2 + c2)2 - 4a2c2 = (a2 - b2 + c2 + 2ac)(a2 - b2 + c2 - 2ac)
b) Si a = 1, b = 2 et c = -1, le second facteur de D est nul. Le système (s2) est donc singulier.

L1 + L3 et L4 fournissent x + z = 1 et -x + z = -2y, d'où z = 1/2 - y ou encore y = 1/2 - z.
L2 + L4 et L1 fournissent y + t = -1/2 et y - t = 1 - 2z, donc y = 1/4 - z
Ces deux résultats sont contradictoires : on retrouve ainsi que (s2) n'admet aucune solution.
4°/ Le système (s1) peut s'écrire matriciellement :

Si X désigne la matrice colonne des inconnues et B celle du second membre, (s1) équivaut à AX = B. La matrice A étant inversible dans le cas présent, on peut multiplier à gauche et à droite par A-1 et on obtient : X = A-1B. il nous suffit donc de calculer A-1.
On a ici D = (a2 - b2 + c2)2 - 4a2c2 = -3.

On remplace d'abord chaque terme aij de la matrice A par son mineur dij. On remarquera que A étant symétrique, on peut gagner un peu de temps... On obtient, avec calme et patience, car une étourderie est vite arrivée :

On multiplie chaque dij par (-1)i+j :

On transpose (la colonne i devient la ligne i) et on divise par le déterminant :

Il vient alors :

On retrouve :
(x, y, z, t) = (-2/3, 4/3, -2/3, 1/3)