
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
 Fils de professeurs de
mathématiques, Paul Erdös fit ses études à Budapest, sa ville natale. Docteur es sciences à 21
ans, il donna à 19 ans une preuve de la conjecture de Bertrand selon laquelle
:
Fils de professeurs de
mathématiques, Paul Erdös fit ses études à Budapest, sa ville natale. Docteur es sciences à 21
ans, il donna à 19 ans une preuve de la conjecture de Bertrand selon laquelle
:
Pour tout entier naturel n au moins égal à 2, il existe un nombre premier entre n et 2n
Désirant compléter sa formation, Erdös s'installe à Manchester (Angleterre). De conferssion juive, l'arrivée du nazisme en Allemagne lui interdit le retour en Hongrie. Il émigre aux États-Unis (1938) bénéficiant d'une bourse à l'université de Princeton. Dix années plus tard, après divers postes sans chaire et accusé de sympathiser avec le marxisme à l'époque du maccarthisme, Erdös dut quitter l'Amérique. Il s'expatrie en Israël. De retour aux USA dans les années 1960, il enseignera dans diverses universités avant de revenir à Budapest.
Les travaux de ce mathématicien ont porté sur le calcul des probabilités, la théorie additive des nombres, la théorie des graphes, ainsi que sur la distribution des nombres premiers pour laquelle il donne (1949), inspiré par les premières avancées de Selberg, une preuve d'une conjecture de Gauss ne faisant pas appel à l'analyse complexe, selon laquelle si π(x) désigne le nombre de nombres premiers inférieurs à l'entier naturel x et ln le logarithme népérien :
![]() (»
réf.4)
(»
réf.4)
Selberg, avec qui il collabora sur ce difficile sujet, publia sa preuve quelques mois avant Erdös, ce qui lui valut la médaille Fields 1950 en engendrant certaines tensions entre les deux mathématiciens (» réf.5c). Élu membre de la Royal Society (à titre étranger) en 1989, Erdös fut récipiendaire, entre autres distinctions, du prix Cole (1951) et du prix Wolf 1983.
» Hadamard , La Vallée-Poussin , Daboussi , Selberg , Maynard
Erdös s'est intéressé aussi aux nombres spéciaux comme les nombres abondants, surabondants (» réf.9), hautement composés, pratiques, puissants, ... en étudiant leur répartition dans l'ensemble des entiers naturels en lien avec celle des nombres premiers.
| Théorèmes : |
Complétant une conjecture de Bertrand, Erdös prouve que :
Pour tout entier naturel n au moins égal à 6, il existe, entre n et 2n, au moins deux nombres premiers, l'un de la forme 4k + 1, l'autre de la forme 4k + 3.
• Les restes de la division par 4 étant 0, 1, 2 ou 3; en tant que nombre impair, puisque n > 6, tout nombre premier de l'intervalle ]n,2n[ est de la forme 4k + 1 ou 4k + 3. L'intérêt du résultat réside dans l'existence de deux nombres premiers de types distincts dans cet intervalle.
» Bertrand , Tchébychev , Ramanujan
➔ π(n) désignant le nombre de nombres premiers inférieurs à n, Tchébychev avait prouvé en 1850 l'inégalité π(2n) > π(n), assurant ainsi l'existence d'un nombre premier entre n et 2n.
La distribution des nombres premiers : »
Toute application non nulle
multiplicative et croissante est complètement
multiplicative et de la forme n → nα
(»
réf.3)
Théorème d'Erdös-Anning (1945, » réf.7) :
Une infinité de points du plan dont la distance entre deux points quelconques est un nombre entier sont alignés.
i Norman Herbert Anning : mathématicien américain (1883-1963), professeur à l'université du Michigan, sise à Ann Arbor. Ses travaux portèrent principalement sur la théorie des nombres et les problèmes soulevés par la théorie des ensembles infinis.
| Conjectures : |
Prolixe et prolifique (plus de 1500 publications, » réf.2), ce célèbre arithméticien se plut à émettre des conjectures, en les accompagnant de prix, et à formuler des théorèmes originaux. Il reçut lui-même pour ses travaux, le prix Wolf 1984.
Sept conjectures d'Erdös, difficiles à prouver mais faciles à énoncer :
Étude de la conjecture & conjecture de Sierpinski : »
➔ la somme des inverses des nombres premiers 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + ... + 1/n + ... étant divergente (» Euler), ce résultat montre en particulier l'existence de nombres premiers en progression arithmétique.
Nombres premiers jumeaux : » Nombres premiers en progression arithmétique : »

Paul Erdös en compagnie
de Claude Berge (1995),
Source INRIA
3. Il existe une infinité de nombres absolument pseudo-premiers (On pseudoprimes and Carmichael numbers, 1956).
Carmichael et nombres absolument pseudo-premiers : »
i Paul Turan (1910-1976), mathématicien hongrois, professeur à l'université de Budapest. Travaux en théorie des nombres en collaboration avec son ami Erdös.
Si M un point intérieur à un
triangle, alors :
et l'égalité ne peut avoir lieu que si le triangle est équilatéral : M est alors l'orthocentre.
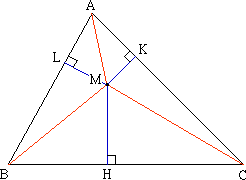
Cette conjecture fut prouvée par Mordell (1937).
Preuve de la conjecture dans le cas équilatéral : » » voir aussi réf.8
6. Conjecture de la discrépance (de l'anglais discrepancy = divergence, discrepancy problem), 1932 et 1957 :
On considère une suite (un) à valeurs dans {-1,1}. En appelant discrépance de cette suite, la borne supérieure pour n et d décrivant N de la somme |ud + u2d + u3d + ... und|, Erdös conjecture que cette borne sup est infinie :
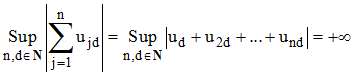
La preuve de cette conjecture a été apportée par Terence Tao en octobre 2015 (» réf.5&6).
7. Dans le cadre de ses recherches sur le "grand" théorème de Fermat, Erdös étudie les nombres puissants (entiers naturels n tels que p2 divise n pour tout facteur premier p de n) et conjecture (1975) qu'il n'existe aucun triplet d'entiers puissants consécutifs. Le problème reste ouvert (juin 2018).
Étude des nombres puissants : »
➔ Pour en savoir plus :