ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
SELBERG Atle,
norvégien, 1917-2007
Médaille Fields 1950 |
Après
des études et l'obtention de son doctorat à l'université d'Oslo (1943), Selberg
y poursuit des recherches en théorie des nombres jusqu'en 1947, année où il
s'expatrie aux USA pour poursuivre ses travaux au déjà célèbre Institute for
Advanced Study de Princeton. Il y sera professeur jusqu'à sa retraite en
1987.
Selberg reçut la médaille Fields en 1950 suite à ses travaux sur l'étude des zéros des fonctions ζ de Riemann (le second récipiendaire fut le français Laurent Schwartz pour sa théorie des distributions) et pour son avancée (1948-49) dans l'étude de la distribution des nombres premiers où il donne, peu avant celle de Erdös, une preuve "élémentaire" du théorème des nombres premiers (arithmétique et analyse dans le champ réel, sans usage des fonctions holomorphes à la manière de Hadamard et de La Vallée-Poussin), dans un mémoire intitulé An elementary proof of the prime–number theorem :
Si
π(x) désigne le nombre de nombres premiers inférieurs à l'entier naturel
x
et ln le logarithme népérien :
et cela quelques mois avant celle, semblable, de Erdös, ce qui engendrera quelques tensions entre les deux mathématiciens sans nuire cependant totalement à leur collaboration sur le sujet (» réf.2). Selberg est aussi lauréat du prix Wolf (1986).
» Gauss , Tchebychev , D. J. Newman , Breusch , Maynard
Identité de Selberg :
La relation ci-dessous fut le point de départ de la preuve de Selberg :
Lorsque p et q désignent des entiers premiers, on a la formule asymptotique (x "grand") :
»
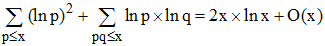O(x) : Landau
i En 1984, le mathématicien tunisien Hédi Daboussi apporte lui aussi une preuve "élémentaire" du théorème (élémentaire pour signifier sans recours à l'analyse complexe) surpassant, par son élégance et son efficacité, la démonstration historique qu'Erdös et Selberg avaient mise au point trente-cinq ans auparavant. (» Hommage à Hédi Daboussi, réf.1).
Hédi Daboussi (1942-2019)
:
mathématicien tunisien qui fit carrière en France après avoir
soutenu sa thèse de doctorat en théorie des nombres, intitulée "Quelques résultats sur les fonctions
arithmétiques", dirigée par Hubert Delange à
la faculté des sciences d'Orsay en 1979.
Tout d'abord professeur à Reims, il rejoint Orsay avant de poursuivre sa carrière à Amiens (université de Picardie). Expert en théorie analytique des nombres, il mit en place à l'Institut Henri Poincaré, à l'instar de son directeur de thèse, un séminaire consacré à cette spécialité. Quelques articles sur les fonctions arithmétiques multiplicatives sont présentes sur Numdam (» réf.3).
➔ Pour en savoir plus :
Ferrand
(Lelong-)