ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 ABU KAMIL
(prononcer Abou Kamil),
égyptien, vers 850-930 |
Cet algébriste égyptien,
de son nom complet Abu Kamil Shuja ibn Aslam ibn Muhammad al-Hasib al-Misri,
surnommé le calculateur égyptien, succède en quelque sorte,
dans la renommée, à
Al-Khwarizmi.
♦ Dans son Livre complet sur l'algèbre, reprenant les concepts de transposition (al jabr) et de réduction (al muqâbalah) de son prédécesseur, il expose 69 problèmes des premier et second degré où il manipule brillamment les radicaux (racines carrées) dont la découverte et les premières manipulations remontent aux Pythagoriciens. Au 13è siècle, Fibonacci, alias Leonard de Pise, le considérait comme le meilleur algébriste arabe et lui emprunta certains résultats.
Abu Kamil présente en particulier (» réf.1, pages 52-60) par des considérations géométriques à la manière d'Euclide, tout comme Al-Khwarizmi, la résolution de l'équation du second degré de la forme :
x2 + p = qx
lorsque les solutions sont positives en discutant selon (q/2)2 > p ou non, ce qui revient à étudier le discriminant de l'équation. Contrairement à ses prédécesseurs, Al-Khwarizmi en particulier, les coefficients des équations étudiées peuvent être irrationnels (radicaux). à ce propos, lorsque a et b sont rationnels (nombres entiers ou fractions), il exprime à quelle condition √a ± √b est la racine carré d'un nombre rationnel :
√a ± √b est un nombre rationnel si et seulement si la racine carrée du produit ab ou du quotient a/b est rationnelle
∗∗∗
Une telle maîtrise des nombres irrationnels se retrouvera chez Abu Bakr Al-Karaji. Sauriez-vous résoudre (» source réf.1) :
∗∗∗
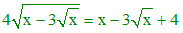
Indications : poser X = x - 3√x, calculer X,
puis poser Y = √x. Solution unique x = 16
Mais Abu Kamil ne se contente pas du second degré. Les problèmes qu'il propose le conduisent à des systèmes d'équations qu'il résout par la méthode de fausse position et de changement d'inconnue l'amenant jusqu'au 4ème degré (équation bicarrée). L'équation du 3ème degré fut étudiée par le philosophe, poète et mathématicien persan Omar al-Khayyam un siècle plus tard.
➔ Les calculs d'Abu Kamil sont exposés verbalement (pas de symbolisme, pas d'influence indienne). Il faudra attendre Al-Kashi à la charnière des 14è et 15è siècles pour un usage systématique du système décimal positionnel, puis Al-Qalasadi au 15è siècle pour celui d'un véritable symbolisme de l'écriture algébrique.
♦ Un second ouvrage propose des calculs à vocation commerciale; il y résout des problèmes concrets se ramenant à des systèmes en nombres entiers à la manière de Diophante d'Alexandrie.
Selon Ahmed Djebbar (» réf.2), Abu Kamil aurait également écrit, à l'instar d'Al-Khwarizmi, un livre sur la résolution algébrique des partages d'héritage, ce qui, dans les droits de succession selon le Coran, n'est pas une mince affaire (» réf.4).
» Aryabhata , Al Qalasadi , Viète
La contribution des sciences arabes
sur
YouTube
conférence de Ahmed Djebbar (en français)
➔ Pour en savoir plus :
,
par Ahmed Djebbar,
Éd. Vuibert/Adapt, Paris - 2005
Al Battani