ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Quadrature du cercle selon Dinostrate       » Quadratrice & trisectrice

Réussir la quadrature d'un cercle, c'est réussir à construire, au sens d'Euclide, un carré de même aire. Supposons son rayon R constructible. Le problème revient à construire un segment de longueur R√π. On sait, depuis Wantzel, que cela n'est pas possible.

Pour Dinostrate, le problème fut de construire un segment de longueur π car la construction de la racine carrée (au sens de Platon et de Euclide : règle non graduée et compas) d'un nombre constructible est aisée : il eut alors l'idée de tracer, point par point, une courbe (nommée quadratrice) permettant une approche mécanique de cette construction :

On peut supposer que le disque est de rayon 1. Le quart de cercle mesure alors π/2, il s'identifie à l'angle ^IOJ. Il s'agit alors de construire un carré de côté √π. Afin de construire notre quadratrice, en notations actuelles, nous considérons un repère orthonormé (O,I,J) :

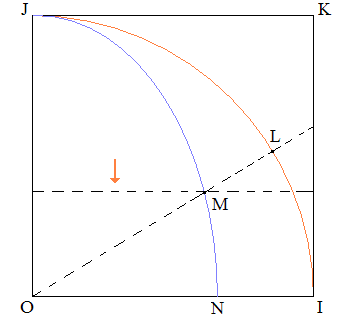
Au temps t = 0, le point L est en J.

On suppose que le côté [JK] du carré OJKI se translate uniformément jusqu'en OI pendant que [OL] tourne uniformément autour de O de sa position initiale jusqu'en [OI] de sorte que les arrivées soient simultanées en un temps t que nous prenons comme unité.

A chaque instant t, on appelle M(x,y) l'intersection de [OL] et du translaté de [JK]. On pose â = ^IOL. Les hypothèses permettent d'écrire les relations et égalités suivantes :

y = 1 - kt, â = π/2 - k't ,  en t = 0 : â = π/2 et y = 1 ,  en t = 1 : â = 0 et y = 0
On en déduit les coefficients de proportionnalité k et k' : y = 1 - t et â = π(1 - t)/2, d'où :

Or lorsque â tend vers 0, on a sensiblement par application de la propriété de Thalès : â/1 = y/x car l'arc MN s'identifie à y et l'arc LI s'identifie à â, LI/OI = MN/ON (cela revient à dire en termes modernes que â/tan â tend vers 1). C'est dire que x tend vers 2/π.

Ainsi, la construction point par point de la quadratrice fournit la construction approchée de 2/π et par suite de 1/π. L'obtention de la construction de π se fait alors par usage de la propriété de Thalès.

 ➔  De y = 2â/π et tan â = y/x, on peut déduire l'équation polaire de la quadratrice en calculant r2 = x2 + y2. On trouvera aisément r2 = 4â2/π2 × 1/sin2â, soit, en posant plutôt ici traditionnellement t = â, une équation de la forme :

r = kt/sint

et on remarquera que c'est l'équation inverse de la cochléoïde.

Inversion géométrique : »
 

Mais comment, à cette époque, tracer avec précision la quadratrice en question ?

Comme les mouvements sont uniformes, à des temps égaux correspondent des arcs et des segments égaux. Donc en t1 = 1/2, [JK] en est à la moitié de son parcours et L est au milieu du quart de cercle : ces points sont constructibles à la règle et au compas, il en est donc de même pour le point correspondant M1 de la quadratrice et, en procédant par dichotomies successives (de moitié en moitié), on pourra alors construire une suite de points médians M2, M3, ..., Mn (autant que nécessaire pour une bonne précision) convergeant vers le point N, en utilisant les temps :

  • t2 = 1/2 + 1/4
  • t3 = 1/2 + 1/4 +1/8,
  • t4 , ...
  • tn = 1/2 + 1/4 + 1/8 + ... + 1/n

car la suite (tn) tend vers 1 (somme des termes d'une suite géométrique de raison 1/2).

 ➔  Pour en savoir plus (constructions diverses et célèbres) :

© Serge Mehl - www.chronomath.com