ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 LISSAJOUS Jules
Antoine,
français, 1822-1880 |
Physicien
dans le domaine de l'optique, ce normalien compléta ces études à la
Sorbonne. Docteur ès
sciences (1850), il fut professeur au lycée Saint-Louis puis recteur
d’Académie (Chambéry, Besançon).
Il étudia les mouvements d'une branche d'un diapason munie d'un petit miroir, l'autre branche étant muni d'un contrepoids calculé pour annuler les effets parasites du miroir sur les vibrations sonores. Un faisceau lumineux tombait sur le miroir et était dévié vers un écran. Un diapason parfait doit fournir le la 3 (fréquence 220 Hz) de façon sinusoïdale. Il constata les contorsions du diapason, comme illustrées par le cas ci-dessous et fut amené à définir les courbes paramétrées, portant son nom, du type :
x = a.sin mt , y = b.cos nt
Une corde vibrante tendue entre deux points (comme celles d'un violon ou d'un piano) ne vibre pas dans un même plan comme on peut le croire à priori mais produit des mouvements similaires selon l'endroit où elle est sollicitée (pincée, frappée ou frottée). Un point donné de la corde (si elle ne se brise pas) décrit une courbe fermée plus ou moins complexe.
Voici sommairement, ci-dessous (merci de votre indulgence), ce que pourrait voir un œil très observateur... :
Le physicien allemand H. L. von Helmholtz, contemporain de Lissajous, étudia la nature du timbre des instruments par la forme de ces courbes de déformation.
On définit généralement les courbes de Lissajous comme pouvant se ramener, à un changement de variable affine près, à la forme :
x = a.sin(mt + α) , y = b.cos(nt + β)
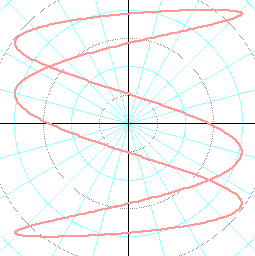
x = sin(3t) , y =
sin(t + π/4)
Pour en savoir un plus sur les courbes de Lissajous : »
Betti