ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Polynômes de
Tchebychev
»
Exercice , Polynômes d'approximation :
généralités |
Il s'agit de polynômes, souvent notés Tn, utilisés dans les approximations polynomiales de fonctions numériques définis sur (ou se ramenant à) l'intervalle J = [-1,1], principalement pour une approximation optimale par un polynôme trigonométrique ou, inversement, pour une approximation rationnelle d'une fonction trigonométrique.
On retrouve également ces polynômes dans des méthodes d'intégration approchée, de résolution d'équations différentielles (issues d'équations aux dérivées partielles), d'accélération de convergence ou d'interpolation polynomiale (amélioration de la méthode d'interpolation de Lagrange). Entre autres possibilités équivalentes, on peut les définir par :
On a To(x) = 1 et T1(x) = x pour tout x de J. Et d'une façon générale :
|
|
On démontre que :
|
|
________
________
1. Montrer que Tn est de degré n , que sa parité est celle de n et que le coefficient de xn est 2n-1
2. Montrer que les zéros (racines) de Tn (n > 0), sur [-1,1] , sont les xk tels que :
, k = 0, 1, ...,
n-13. Approcher une fonction f sur un intervalle J par ces polynômes, c'est l'écrire sous la forme :
dans l'espace de Hilbert des fonctions continues sur [-1;1] muni du produit scalaire :
Pour des raisons de commodité de calcul, il serait bon que les Tk soient orthogonaux, voire normés : ils constitueraient alors un système orthonormal et dans ce cas, le calcul d'un coefficient ai dans le développement de f sera donné par :
a/ en utilisant que cos(m + n)t + cos(m - n)t = 2cos mt.cos nt, montrer que si m et n sont distincts :
b/ en utilisant que Tn(cost) = cos nt et en posant ci-dessus x = cos t, loisible puisque cos est strictement décroissant sur [o,π], montrer que :
puis que :
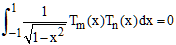
Donc, si nous définissons dans la forme :
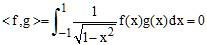
les polynômes de Tchebychev constituent une famille orthogonale pour ce produit scalaire.
» Dans ces types de produit scalaire sur des espaces de fonctions où il a fallu pondérer par une fonction Φ pour obtenir un système orthogonal, on dit que Φ est une densité ou encore une fonction de poids. Ici Φ(x) = 1/√(1 - x2). Pour les polynômes de Legendre, Φ est tout simplement 1 (constante).
» Densité associé à un produit scalaire
Afin d'obtenir un système orthonormal, compte tenu que l'intégrale sur [o,π] de cos2nt est π/2, il suffit de considérer, au lieu des polynômes Tn les polynômes définis par :
