
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

John Farey n'est pas un mathématicien mais un géologue dont le nom se retrouve dans une curiosité arithmétique liée aux fractions élémentaires, les suites de Farey, qui ont été étudiées sous une forme géométrique au 20è siècle par le mathématicien américain Lester R. Ford Sr (père) : cercles de Ford.
| Suites de Farey (Bulletin de la Société philomatique, Paris, 1816) : |
Si l'on écrit successivement, en ordre croissant, toutes les fractions irréductibles de l'intervalle [0,1] dont le dénominateur n'excède pas un entier donné, on observe une curieuse propriété :
•
Pour deux fractions consécutives
![]() et
et
![]() , la différence
des produits "en croix" bc - ad est toujours égale à 1.
, la différence
des produits "en croix" bc - ad est toujours égale à 1.
•
L'insertion de la fraction
![]() , obtenue en
ajoutant entre eux les numérateurs et les dénominateurs de
, obtenue en
ajoutant entre eux les numérateurs et les dénominateurs de
![]() et
et
![]() , fournit une
fraction vérifiant la propriété précédente et toujours
comprise entre
, fournit une
fraction vérifiant la propriété précédente et toujours
comprise entre
![]() et
et
![]() .
.
➔
Et notant
Sn la suite associée à un entier n, cette dernière propriété permet
alors de construire la suite Sn+1 en insérant les fractions
![]() tant que b + d
ne dépasse pas n + 1 :
tant que b + d
ne dépasse pas n + 1 :
Considérons le cas n = 5 : afin de construire la suite, on écrit :
0/1 et 1/1;
puis la famille des cinquièmes : 1/5 , 2/5 , 3/5 , 4/5;
on insère la famille des quarts : 1/4 , 2/4 = 1/2 , 3/4;
puis la famille des tiers : 1/3 , 2/3;
enfin la famille des demis : mais 1/2 est déjà inscrit.
![]()
On obtient S6 par insertion :
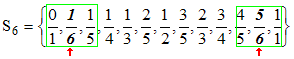
Puis S7 :

etc.
Farey observa le phénomène mais reconnut ne pas en trouver d'explications. Il fut justifié par Cauchy. Lester R. Ford Sr en donna une explication géométrique au siècle suivant.
Fractions unitaires (ou fractions égyptiennes) : »
➔ Pour en savoir plus :
Ce qu'en dit Edouard Lucas dans sa théorie des nombres (1891) : http://gallica.bnf.fr/ark:/12148/bpt6k29021h/f256.table
Suites de Farey et hypothèse de
Riemann par Charles Pisot sur
Numdam :
http://archive.numdam.org/article/SDPP_1960-1961__2__A11_0.pdf
» Charles Pisot Hypothèse de Riemann : »