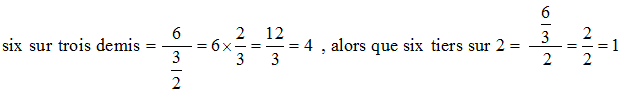ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
|
Si l'écriture multiplicative :
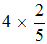
ne présente aucune ambiguïté, il n'en est pas de même de :
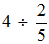
Cette dernière écriture doit signifier 4 ÷ (2/5) = 4 ÷ 0,4 = 10 et surtout pas (4 ÷ 2)/5 = 2/5.
L'écriture fractionnaire a/b représente une division (un quotient) non effectué et iviser a par b (a ÷ b), c'est multiplier a par 1/b.
5/4 c'est "cinq quarts" donc 5 fois 1/4 :
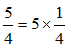 : on multiplie 5
par l'inverse de 4.
: on multiplie 5
par l'inverse de 4.
L'inverse d'une fraction a/b est la fraction b/a : au lieu d'écrire le quotient de a par b, on inverse le numérateur et le dénominateur et on obtient le quotient de b par a :
L'inverse de 5/4 est 4/5.
L'inverse de 2 est 1/2 car 2 peut s'écrire 2/1 : diviser par 1 ne sert à rien... Ok ?
» On retient : diviser c'est multiplier par l'inverse :

! Que dire de 4 ÷ 2 ÷ 5 ? La règle usuelle selon laquelle, en l'absence de parenthèses, on effectue les calculs dans l'ordre d'écriture peut être appliquée. Donc, 4 ÷ 2 ÷ 5 = (4 ÷ 2) ÷ 5 = 2 ÷ 5 = 0,4, et non plus à 10 !
Autre difficulté :
Avec l'écriture fractionnaire usuelle, en cas de division, le professeur rappelle aux élèves de faire apparaître des barres de fraction de longueur différente. Cette écriture, par exemple, n'a pas de sens :
« 4 sur
![]() » ne s'écrira pas
» ne s'écrira pas
![]()
car que veut-elle signifier :
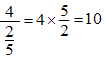 ?
ou bien :
?
ou bien :
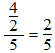 ?
?
➔
On retrouve, dans ce risque d'erreurs, celles faites par les élèves utilisant
leur calculatrice sans trop connaître les règles de priorité : soit à calculer
par exemple 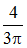 : il s'agit de diviser 4 par le produit 3π, c'est à
dire 4 divisé par 3, puis le résultat divisé par π :
(4 ÷ 3) ÷ π.
: il s'agit de diviser 4 par le produit 3π, c'est à
dire 4 divisé par 3, puis le résultat divisé par π :
(4 ÷ 3) ÷ π.
Si l'on tape 4 ÷ 3 × π, on obtient :

Ce qui n'est pas le calcul proposé ! Il faut taper :
4 ÷ (3 × π) ou encore 4 ÷ 3 ÷ π
Une chance cependant avec les calculatrices récentes utilisées aujourd'hui au collège : les écritures 4 ÷ 3π ou encore 4 ÷ 3√2 conduisent au résultat voulu : les constructeurs ont en effet prévu que l'absence du signe multiplicatif dans ce type d'écriture rend prioritaire la multiplication implicite :
3π = 3 × π , 3√2 = 3 × √2
et nombreux sont les élèves qui "font juste" en pensant faux... :
4 ÷ 3π et 4 ÷ 3√2 sont reconnus respectivement comme 4 ÷ (3 × π) et 4 ÷ (3 × √2)
D'une façon générale, puisque diviser c'est multiplier par l'inverse :
diviser par x c'est multiplier par 1/x et diviser par x/y c'est multiplier par y/x
Application :
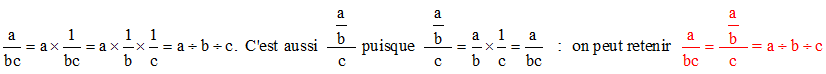
» La dernière
égalité est pratique en cas d'usage de la calculatrice : dans le calcul
précédent de 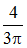 , on
tape 4 ÷ 3 ÷ π
, on
tape 4 ÷ 3 ÷ π
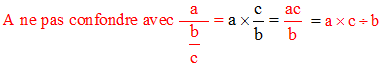
Exemple final :