ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Parallèles d'une courbe     » cas de l'ellipse | cas de la parabole | toroïde

Étant donnés une courbe (Γ) et un réel k, on appelle parallèle de paramètre k à la courbe (C) l'enveloppe des cercles de rayon k centrés en un point M de (C) lorsque ce point parcourt la courbe. La recherche de l'équation des courbes parallèles est semblable à celle décrite pour les enveloppes de droites. Cette enveloppe est généralement double.

Étude :   

On suppose que (Γ) admet une représentation paramétrique de paramètre m et admet une tangente en chacun de ses points. Dans ces conditions, notons x = f(m) et y = g(m) les coordonnées d'un point M_m de (Γ) et considérons deux cercles suffisamment proches C_m et C_m+h centrés en M_m et M_m+h :

Ces cercles se rencontrent en deux points A et B; leur axe radical (AB) est perpendiculaire à la ligne des centres (M_mM_m+h). Lorsque h tend vers 0, La droite ((M_mM_m+h) tend vers la tangente en M_m à la courbe et (AB) devient la normale (n) à la courbe (Γ).

Par conséquent, les points caractéristiques de l'enveloppe cherchée sont les points de la normale en M_m, extrémités du diamètre du cercle de centre M_m, de rayon k : (C) et sa parallèle de paramètre k ont les mêmes normales.

Ci-dessous :   

• on a tracé l'ellipse de foyers F et F', de de demi grand axe a, de demi petit axe b, b < a.

• on a choisi k > b; dans ces conditions, on obtient deux courbes parallèles en vert (parallèle extérieure) et en bleu (parallèle intérieure). La parallèle extérieure correspond à l'idée intuitive d'une courbe parallèle...

Cette courbe est-elle une ellipse ?   

Non ! cette forme « ovale » correspond à une courbe algébrique f(x²,y²,k) = 0 du 8è degré (biquartique) : l'équation cartésienne est épouvantable mais l'équation paramétrique est facile à établir :

Partons d'une ellipse (E) sous sa forme paramétrée : x = a.cost , y = b.sint. Un vecteur directeur de la tangente en un point P de (E) est u(1;dy/dx).

Par suite, un vecteur directeur de la normale en P est n(-dy/dx;1), soit n(cotant × b/a;1), cotan désignant la fonction cotangente (cos/sin) inverse de la fonction tangente. L'équation paramétrique de la normale en P, d'angle polaire t, est alors :

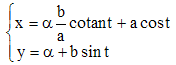
où α décrit R. Si M est un point de la parallèle correspondant au point P de (E), M est sur la normale en P de sorte que MP² = k²; par conséquent :

On en déduit α en fonction de a, k et b puis l'expression de x et y :

Plus généralement :    

Si la courbe donnée (Γ) est paramétrée par x = f(t) et y = g(t), un calcul semblable conduit sans difficultés à l'équation paramétrique des courbes parallèles (attention aux signes opposés) :

 ➔    Suivant les valeurs de a, b et k, la courbe parallèle intérieure prendra diverses formes.

On pourra tester cela avec la figure CabriJava :  »

» Selon un petit fascicule de la Revue du Palais de la découverte, réédition (décembre 1995) d'un album de courbes paru en 1937, cette courbe fut étudiée par un certain Breton-dès-Champs et prit le nom de toroïde (mot à mot : en forme de tore) en 1884. H. Brocard et T. Lemoyne, dans leur traité COURBES GÉOMÉTRIQUES REMARQUABLES (Librairie scientifique et technique Albert Blanchard - Paris 1919 - Rééd. 1967), parle de Breton de Champ. Des recherches sur la BNF, site Gallica, indiquent qu'il s'agit de :

 i  Paul Emile Breton de Champ (1814-1885), polytechnicien, ingénieur des ponts & chaussées et éminent géomètre (travaux sur les courbes et surfaces). L'appellation toroïde semble justifiée : si l'on considère l'ensemble des cercles engendrant les courbes parallèles de l'ellipse, on croit voir la perspective d'un tore.

On a choisi ici la parabole d'équation y = x² tracée en bleu. Les parallèles de paramètre k = 2 sont tracées en rouge. On peut paramétrer la courbe en posant tout simplement :

x = f(t) = t , y = g(t) = t²

On a alors f '(t) = 1 et g'(t) = 2t. Ces égalités conduisant à l'équation paramétrique des parallèles cherchées :

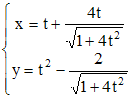    et