ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Comportement en zéro de f(x) = sin(x)/x               » Quatre limites classiques

On pose :

et on se propose de montrer que f est dérivable en zéro (donc continue en 0. Pour ce faire, on va établir un encadrement polynomial de la fonction sinus car il n'est pas possible d'établir la dérivabilité de f en zéro au seul moyen du résultat de référence, connu dès la classe de première, selon lequel la limite en zéro de la fonction x → sin(x)/x est égale à 1.

 ➔  On remarquera que la méthode revient à utiliser (niveau bac+1) le développement limité à l'ordre 3 de la fonction sinus : sin x = x - x³/6 + o(x⁵)

1°) Montrer, en étudiant le sens de variation de la fonction δ : x → sin x - x, que :

On pose maintenant, pour tout x réel :

2°) Calculer les dérivées première, seconde et troisième de g. Vérifier que g'''(x) = 1 - cos x. Compléter alors le tableau de variation ci-contre (valeurs en zéro et sens de variation) et établir que pour tout x positif, on a g(x) ≥ 0.

3°) Eu égard à 1° et 2°, il est donc établi que :

Rappel :

Si f est dérivable en zéro, alors :

où T est le taux d'accroissement de f au voisinage de zéro, à savoir :

Il est clair que la fonction f, objet de notre étude, est paire : son comportement en 0 peut se restreindre à x > 0. Vérifier que

et montrer par encadrement de T au voisinage de 0⁺ et passage à la limite, que f est dérivable en 0 (et, par là, continue en 0) et que sa dérivée est nulle en ce point (utiliser 3° en appliquant le théorème du "sandwich", également appelé théorème des gendarmes : encadrement serré...).

Complément :    

En tout point autre que 0, la fonction dérivée de f est (x.cosx - sinx)/x². Cette dérivée s'annule en changeant de signe en tout point x = tanx, d'ordonnée cosx.

Interprétation graphique de l'équation x.cosx - sinx = 0 : intersections de [y = x] et [y = tanx]

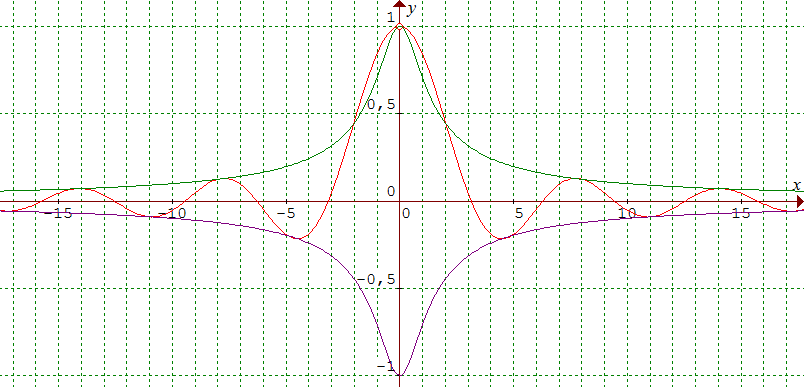
La courbe représentative de f est une sinusoïde amortie :

   

On remarquera que les extrema de f se situent sur la courbe ensemble des points M(tanx, cosx) dont une équation cartésienne est y²(x² + 1) = 1 et représentée en vert et violet ci-dessous :

Calcul de l'intégrale de sin(x)/x sur [0,+∞[  au moyen d'une intégrale curviligne : »

 

Ces trois limites interviennent fréquemment en analyse. Elles sont prouvées par ailleurs à partir de considérations géométriques : application, encore..., du théorème des gendarmes. L'étude précédente permet de les retrouver :

En effet, l'étude prouve que f est continue en 0 car, par définition de la notion de dérivée :

Toute fonction dérivable en un point est continue en ce point.

On peut donc affirmer que :

Sans passer par la dérivée, le résultat obtenu en 3° peut s'écrire, pour tout x strictement positif :

On en déduit par passage à la limite :

Cette fonction étant paire puisque sin(-x) = -sin(x), le résultat est encore valable en 0^-. D'où le résultat.

En multipliant par 1/cosx tendant vers 1, on déduira de ce résultat :

Posons maintenant :  

Si nous voulons passer à la limite en 0, le 1er facteur tend vers 2, le second prend la forme indéterminée 0/0. Mais on peut écrire :

Sous cette forme, il apparaît que la limite en 0 de h est 0 × 1 = 0. Et comme 1 + cosx tend vers 2, on peut en conclure :