ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Fonctions Arc sinus & arc
sinus
»
Arc cosinus , Arc
tangente |
Nom de la fonction :
Arc sinus.
C'est une fonction
trigonométrique, fonction réciproque
de la
fonction sinus
restreinte à l'intervalle J =
[-π/2,
+π/2]
sur lequel cette dernière est bijective puisque continue et strictement
croissante de J sur [-1,+1].
Origine du nom : abréviation de sinus et de arc (de cercle). L'Arc sinus d'un nombre x est l'angle y (exprimé en radians) de l'intervalle [-π/2, +π/2] dont le sinus est x.
Ensemble de définition : [-1,+1].
Notation : y = Arcsin
(x),
Asin(x) ou
encore
y = Asn(x).
y = Arcsin(x) ⇔ x = sin y
Exemple : Arcsin(1/2) = π/6.
Pourquoi Arc et non angle ? Tout simplement parce que sur le cercle trigonométrique (centré à l'origine et de rayon 1), y représente la mesure de l'arc AM défini par l'angle ^AOM.
Périodique : non.
Fonction dérivée :
Nom de la courbe associée : néant. Mais, par symétrie, c'est un arc de sinusoïde.
Applications : recherche d'un angle dont le sinus est donné. Touche sin-1 ou Asn des calculatrices.
|
Plus généralement, la fonction asn : |
Si on a l'égalité x = sin y, on notera y = asn x (ou y = arc sin x), sans majuscule, les nombres y dont le sinus est x : c'est une fonction multiforme (infinité d'images).
En effet, la fonction sinus a pour période 2π et, de plus sin y = sin(π - y), donc :
Si x = sin y, on a aussi x = sin(y + 2kπ) et x = sin(π - y + 2kπ)
C'est dire, par exemple que asn(1/2) a pour images π/6 , 5π/6 , 13π/6 , 17π/6 , ...
∗∗∗
Dans
le bon vieux temps des années 1980, les matheux faisaient de la programmation :
on n'avait pas encore Mathematica ou Maple.
Les langages comme
BASIC sur Apple ou MS-DOS ne possédaient que la fonction ATN (Arc tangente), d'où
l'astuce :
Vérifier que l'instruction
u = 2*ATN(x/(1 + sqr(1 - x*x)) retourne Asn(x) dans la variable
u.
∗∗∗
Étude d'une
fonction Arc sinus un peu compliquée...
| Fonctions Arc cosinus
& arc cosinus |
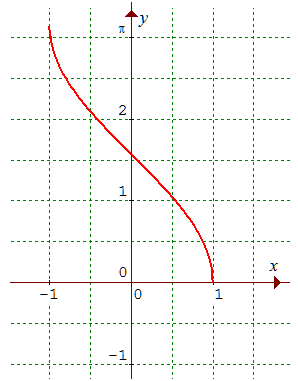
Nom de la
fonction : Arc
cosinus.
C'est une fonction
trigonométrique, réciproque de la
fonction cosinus
restreinte à l'intervalle J =
[0,
π] sur lequel
cette dernière est bijective puisque continue et strictement décroissante de
J sur [-1,+1].
Origine du nom, abréviation : de cosinus et de arc (de cercle). L'Arc cosinus d'un nombre x est l'angle y (exprimé en radians) de l'intervalle [0, π] dont le cosinus est x.
Ensemble de définition : [-1,+1].
Notation : y = Arccos(x) ou y = Acs(x).
Exemple : Arccos(1/2) = π/3.
Pourquoi Arc et non angle ? Tout simplement parce que sur le cercle trigonométrique (centré à l'origine et de rayon 1), y représente la mesure de l'arc AM défini par l'angle ^AOM.
Périodique : non.
Fonction dérivée :
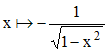
Nom de la courbe associée : néant. Mais, par symétrie, c'est un arc de sinusoïde.
Définition équivalente : fonction réciproque (aussi dite, à tort, fonction inverse) de la fonction cosinus restreinte à l'intervalle J = [0,π] sur lequel cette dernière est bijective : continue et strictement décroissante de J sur [-1,+1].
Applications : recherche d'un angle dont le cosinus est donné. Touche cos-1 ou Acs des calculatrices.
| Plus généralement, la fonction acs : |
Si on a l'égalité x = cos y, on notera
y = acsx (ou y = arccos x),
sans majuscule, les nombres y dont le cosinus est x : c'est
une fonction multiforme (infinité d'images).
En effet, la fonction cosinus a pour période 2π et, de plus cos y = cos(- y), donc :
Si x = cosy, on a aussi x = cos(y + 2kπ)
et x = cos(2kπ - y)
C'est dire, par exemple que acs(1/2) a pour images π/3 , -π/3 , 13π/3 , 11π/3 , ...
∗∗∗
Dans
le bon vieux temps des années 1980, les matheux faisaient de la programmation :
on n'avait pas encore Mathematica ou Maple.
Les langages comme
BASIC sur Apple ou MS-DOS ne possédaient que la fonction ATN (Arc tangente), d'où
l'astuce :
Vérifier que l'instruction
u = 1.5707963267949897 - 2*ATN(x/(1 + sqr(1 -
x*x)) retourne Acs(x)
dans la variable u.
∗∗∗
Prouver que : 2Acs(3/4) = Acs(1/8)
| Remarques : |
Puisque cos x = sin(π/2 - x), on remarquera que :
Arcsinx + Arccosx = π/2
D'autre part, cos2(Asin(x)) + sin2(Asin(x)) = 1, donc :
Si -1 ≤ x ≤ 1, cos(Asinx)
= √(1 - x)2
On a aussi
cos2(Acos(x))
+ sin2(Acos(x))
= 1, donc :
Si -1 ≤ x ≤ 1, sin(Acos(x)) = √(1 - x)2