
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Cotangente , sinus , cosinus , sécante & cosécante Arc sinus & Arc cosinus , Arc tangente & Arc cotangente Sinus & cosinus hyperboliques , tangente & cotangente hyperboliques |
| Définitions possibles : |
tan(x) = sin(x)/cos(x)
Plus géométriquement, dans un repère orthonormé (O,I,J) orienté par le sens trigonométrique usuel (sens inverse des aiguilles d'une montre) , soit M un point en rotation sur un cercle centré en O, de rayon 1 (cercle trigonométrique). Avec ces notations, la tangente de l'angle x est la mesure algébrique IT du segment de tangente en I sur le schéma coupant [OM) en T :

Cette définition au moyen du cercle trigonométrique confère à la fonction
tan le nom de
fonction circulaire, au
nombre de trois avec sinus et
cosinus,
voire quatre si on tient compte de la cotangente
cotan(x) = 1/tan(x).
»
En application du théorème de Thalès, on a
AT/HM
= OA/OH.
Or OA
= 1, HM
= sin(x) et OH = cos(x) : on retrouve
la définition bien connue : tan(x) = sin(x)/cos(x).
Dans un triangle ABC rectangle en A, la
tangente d'un angle aigu (^B ou ^C) est égal au quotient (des mesures) du côté
opposé par le côté adjacent. Par exemple, tan^B = AC/AB.
On peut écrire AC/AB = AC/BC × BC/AB
= (AC/BC)/(AB/BC) : on retrouve tan(^B) = sin^B/cos^B.
Remarque :
Sur la figure ci-dessous, complétée de la précédente, les segments de tangente [IT] et [ML] ont même mesure (il est facile de prouver cela en considérant les triangles rectangles OIT et OML). Par conséquent, dans le cas de l'angle aigu, on retrouve tan(x) en ML. On retrouve de même cotan(x) en MN.

! Cette remarque ne doit pas inciter le lecteur à utiliser ces mesures car dans le cas d'un angle obtus, on perd l'information du signe. Concernant la tangente, [IT) est une demi-droite orientée, parallèle à (y'y). Par exemple, si x = 2π/3 (120°), on aura tan(x) = IT < 0 car [OM) coupe la tangente en I "sous" l'axe des abscisses et [IT) a alors même sens que (Oy').
| Représentation graphique : |
Lorsque x (exprimé en radians) tend vers π/2 (soit 90°), IT devient infini, ce qui explique la présence d'un asymptote verticale en ce point pour la courbe représentative de la fonction tan.
Sur le graphique, l'axe des abscisses porte la mesure, en radians de l'angle (OA,OM). Les asymptotes verticales apparaissent lorsque cos x = 0, donc en x = π/2 + kπ, k ∈ Z, soit : x = ± π/2, ± 3π/2, ± π/2...
Par application du théorème de Thalès dans le triangle OAT, il apparaît que HM / AT = OH / OA. Mais OA = 1, OH = cos(x) et HM = sin(x). D'où la définition donnée en 1°.
La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Déplacer le point P : la courbe
tangente x → tan(x) apparaît
en
rouge
| Applications : |
La tangente est apparue chez les mathématiciens hindoues et transmise aux Arabes. C'est à Abu al Wafa que l'on doit la définition actuelle. Elle apparaît, en particulier, de façon naturelle dans tous les calculs d'atelier (construction, tournage, fraisage, engrenages, ...) où la trigonométrie (au sens premier mesure des angles d'un triangle) intervient.
|
Formules élémentaires, valeurs remarquables : |
•
 •
•
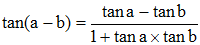
•

•
 •
•

•

•
 »
preuve •
»
preuve • 
• tan a = tan b ⇔ a = b + kπ, k∈Z
• tan(-a) = - tan a • tan(a + π) = tan a • tan(π - x) = - tan(x)
• tan(π/6) = 1/√3 = √3/3 , tan(π/4) = 1 , tan(π/3) = √3 , tan(2π/3) = - √3
• Concernant les tangentes des angles π/5 (36°) , 2π/5, π/10 (18°), 3π/10 » pentagone et décagone réguliers
• Concernant la tangente de π/12 (15°) »
cliquez-moi
∗∗∗

|
Autres formules pratiques (paramétrisation des lignes trigonométriques) : |
Si on pose t = tan(x/2), on a 1 + t
2 = 1 + sin2(x/2)/cos2(x/2) = 1/cos2(x/2) et tan(x) = tan(2 × x/2). On vérifiera alors aisément les formules suivantes permettant l'usage d'expressions rationnelles, tout particulièrement en calcul intégral :

La fonction Arc tangente, réciproque de tan sur l'intervalle ]-π/2,π/2[ :
»∗∗∗
1 Dans un repère orthonormé, dessiner le cercle (c) de centre I(2,1) de rayon 1 et le cercle (c') de centre J(6,2) de rayon 2. On note (T) la droite tangente à (c) et (c') autre que (x'x). Calculer au moyen de votre calculatrice la valeur exacte du coefficient directeur de (T) sachant que celui-ci est un rationnel simple. On rappelle que le coefficient directeur d'une droite d est la tangente de l'angle (Ox,d).
2
a) Donner le
développement (1 +
√3)2
b)
Résoudre
l'équation : 4sin2x + 2(1 -
√3)sin x - √3
= 0
3 L'objectif est de résoudre l'équation (e) : √2cos 2x + sin 2x - 2cos2x = 0 (Dakar, ex. bac 1ère CE 1982)
a) Vérifier que x =
π/2 + kπ,
k entier, n'est pas solution de l'équation.
b) En remarquant que π/4 est le double de
π/8 et en utilisant les formules de duplication du
sinus et du
cosinus, montrer
que tan π/8 =
√2 - 1.
c) Montrer que l'équation (e) se ramène à : (√2
- 2)cos2x - √2sin2x
+ 2sin x.cos x = 0. Poser alors X = tan x et prouver
que X = 1 ou
X = √2 - 1.
d) Déduire des questions précédentes que les solutions de l'équation (1)
sont, à kπ près, π/4
et π/8.
4 Charpente métallique 5 Hauteur d'un immeuble