
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Également rencontré dans certains pays arabes sous le nom de Al-Karkhi pour signifier originaire de Karkh, un faubourg au sud de la florissante ville de Bagdad, fondée en 762 par le calife abbasside Abu Jafar Al-Mansour (714-775). Cependant, selon les historiens, cet algébriste et architecte spécialisé en adduction d'eau (canaux et aqueducs) serait sans doute né à Karaj en Iran, à l'ouest de Téhéran et venu s'installer dans cette ville de l'Irak, attiré par le rayonnement culturel de Bagdad, dont le calife Abd Allah Al-Mahmoun (813-833) fut l'artisan à l'époque du célèbre algébriste Al-Khwarizmi.

La ville ronde de Bagdad au 8è siècle - Source :
Institut
du Monde Arabe (» réf.1b)
Al-Karaji ne fut connu en Occident qu'au milieu du 19è siècle grâce aux recherches de Franz Woepcke (1826-1864), orientaliste et historien des sciences allemand (» réf.2). Il écrivit de nombreux ouvrages en qualité d'ingénieur et, en mathématiques, il nous est désormais principalement connu par trois ouvrages don il est fait état ci-après :
Al-Kafi fi'l-hisâb (Le livre complet sur le calcul) :
70 chapitres dont la première partie est inspirée de son contemporain Abu l'Wafa, portant sur l'arithmétique et les calculs commerciaux, en développant les opérations sur les fractions, l'usage des proportions appliquées à la règle de trois, un sujet traité à la même époque par Al-Biruni, les preuves par 9 et 11, des exemples de résolution de problèmes concrets se ramenant au 1er degré. Quelques chapitres de ce livre sont consacrés à la géométrie élémentaire.
Kitab al-Fakhri fi'l-jabr (Le livre glorieux en algèbre) :
Écrit vers 1010/1012, ce livre est dédié à son vizir et protecteur Fakhr al-Mulk établi à Bagdad dans la période 1010-1015. Dans cet ouvrage novateur, Al-Karaji présente la première théorie du calcul algébrique polynomial s'affranchissant du support de la géométrie. Il expose pour la première fois le concept abstrait de monôme et de polynôme qu'il manipule parfois en tant que le n-uplet de ses coefficients, tout comme on le fait de nos jours :
P(x) = anxn + an-1xn-1 + … + a1x + ao ↔ (an , an-1 , … , a1 , ao
et auxquels il applique les opérations arithmétiques (addition, soustraction, multiplication, proportions). Les spécialistes parlent d'arithmétisation de l'algèbre (» ref.3). La notion de puissance de l'inconnue (nommée cheï, la chose, comme chez Al-Khwarizmi) est généralisée par la récurrence xn = xn-1 × x, tout comme pour son inverse 1/x. Les règles x × 1/y = x/y, 1/x × 1/y = 1/xy ainsi que 1/x ÷ 1/y = y/x sont exprimées et commentées. Mais les nombres négatifs et le zéro, présents dans les mathématiques indiennes depuis plus de 350 ans, sont absents. Ce qui oblige l'auteur, en présence d'une équation, à étudier plusieurs cas à la manière d'Al-Khwarizmi.
Par exemple, l'équation ax2n + bxn
= c, qu'il ramène au second degré en posant X = xn, nécessite
deux autres cas d'étude, à savoir
ax2n + c = bxn et ax2n = bxn + c.
Quasiment aucun symbolisme; les nombres et les équations sont écrits/décrites verbalement. Il faudra étonnamment attendre le 13è siècle, avec Al-Banna pour un premier usage de symboles algébriques dans les mathématiques arabes, usage qui sera conforté par Al-Qalasadi 150 ans plus tard.
La finalité de l'auteur réside dans la recherche de méthodes générales de résolution de problèmes algébriques lesquels consistent, comme il l'écrit, à déterminer des quantités inconnues à partir de quantités connues (coefficients, paramètres), éventuellement irrationnelles (radicaux), en précisant les conditions d'existence des solutions. Il ne s'agit plus de résoudre des équations à la manière d'Al-Khwarizmi en présentant divers cas pratiques s'appuyant sur une interprétation géométrique (calculs d'aires en particulier). La fin de l'ouvrage est consacrée à la résolution d'équations algébriques s'appuyant notamment sur Abu Kamil et Diophante d'Alexandrie en excluant nullement, contrairement à ce dernier les solutions irrationnelles.
à ce sujet, Al-Karaji exprime des formules sophistiquées relatives aux radicaux arithmétiques. Par exemple :
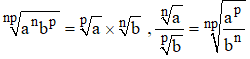

» As-Samaw'al , Abu Kamil , At-Tusi , Al-Kashi
Al-Badi fi'l-hisâb, Le livre novateur en calcul :
Postérieur au précédent, ce livre reprend un grand nombre de propositions arithmétiques des Éléments d'Euclide. Al Karaji expose ensuite de nombreuses formules calculatoires relatives aux radicaux et à diverses expressions irrationnelles, et étudie, entre autres sujets, les polynômes pouvant s'écrire P(x) = [Q(x)]2 ou encore l'équation P(x) = u2 où u désigne un rationnel donné. Le livre se termine par la résolution de systèmes d'équations avec paramètres, par exemple :
♦
(» réf.2)
♦ x2 + y2 = z2 , xz = y2 , xy = 10 (» réf.3)
| Le triangle arithmétique : |
Dans ses calculs algébriques, Al-Karaji est amené à développer des formes du type (a + b)n. Abu Nasr As-Samaw'al qui vécut au 12è siècle est l'auteur du Livre flamboyant de l'algèbre (Kitab al-bahir fi l-jabr) dans la continuité des travaux d'Al-Karaji. Son manuscrit, retrouvé dans la bibliothèque de la basilique Sainte-Sophie (Aya Sophya) d'Istanbul, contient un tableau correspondant à ce que l'on appelle communément en occident le triangle arithmétique de Pascal, permettant le calcul rapide de (a + b)n développé jusqu'à la puissance 12. As-Samaw'al dit le tenir d'Al-Karaji, mais le manuscrit de ce dernier ne nous est pas parvenu. Les coefficients sont écrits en base 10 avec usage du zéro, système décimal positionnel, que privilégia cet algébriste, contrairement à son prédécesseur.
Le triangle se lit de droite à gauche.
Le codage de la première ligne exprime les puissances successives :
aucune , carré (2), cube (3), carré-carré (4),
carré-cube (5), ..., jusqu'à la 12è puissance :
cube-cube-cube-cube.
La 3ème ligne est constituée des chiffres et nombres arabes de 1 à 12.
La 6è colonne indique de haut en bas : 1 6 15 20 15 6 1, soit :
(a + b)6 = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6

Source image : ResearchGate, Archive for Hisory of Exact
Sciences, juin 2015,
»
réf.7
Le principe de construction du "triangle" décrit par Al-Karaji (» réf.7, pages 17-20) est conforme à la formule de récurrence s'écrivant de nos jours par :

|
|
|
|
|
|
|
|
|
|
|
9 |
10 |
11 |
12 |
|
|
|
||||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
9 |
1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |||
|
10 |
1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | ||
| 11 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | |
| 12 | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 |
Al-Karaji conjectura la formule de la somme des n premiers carrés d'entiers sous la forme (» réf.3a, pages 60) :

Ce qui équivaut à :
 (Σ2)
(Σ2)
La formule sera démontrée par As-Samawal. On en trouvera une preuve sur cette page. On peut aussi procéder par récurrence, dont Al-Karaji fut, avec As-Samaw'al, un précurseur bien avant Maurolycus et Pascal (» on pourra consulter à ce sujet l'article de Roshdi Rashed, historien des sciences, en réf.8) :
La formule est manifestement exacte pour n = 1;
Supposons la formule vérifiée pour un entier
n au moins égal à 1 et considérons la somme S = 12 + 22
+ ... + n2 + (n+1)2;
nous pouvons écrire S = n(n + 1)(2n + 1)/6 + (n + 1)2 = (n + 1)
× [n(2n + 1) + 6(n + 1)]/6 = (n + 1) × (2n2 + 7n + 6)/6.
Le trinôme du second degré n'est autre que 2(n + 2)(n + 3/2) = (2n + 3)(n +
2). Donc S = (n + 1)(n + 2)(2n + 3)/6 : ce qui établit la formule au rang n
+ 1.
La formule (Σ2) est donc vraie pour tout n ≥ 1.
Mathématiques & Islam : »
➔ Pour en savoir plus :