ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 RUDOLFF
(RUDOLFFEN) Christoff,
allemand, vers 1500?-1545? |
Christoff Rudolff étudia à l'université de Vienne (Autriche). On lui doit un remarquable traité d'algèbre, intitulé Die Coss (1525), c'est à dire l'inconnue imprimé à Strasbourg, mot forgé sur le mot italien (et espagnol) cosa = la chose.
Université de Vienne -
Source photo :
http://www.gor.de/gor09/index_en.php
Abandonnant le latin, ce fut le premier traité d'algèbre en langue allemande. Cependant à la même époque, son compatriote Adam Riese écrira, en allemand également, un traité (non publié) sous le même nom dont le symbolisme algébrique sera pérennisé.
L'année suivante (1526), dans un traité
d'arithmétique, Rudolff est à l'origine de la notation actuelle pour les radicaux arithmétiques (racines
carrés, cubiques, n-èmes) :
Cette sorte de v, n'est-il pas en fait un r minuscule manuscrit déformé ?
Sans aucun doute, car la notation R, pour racine, du latin radix, radice (en italien), root (en anglais) était utilisée par les grands algébristes contemporains, italiens en particulier, comme Cardan puis Bombelli. La notation de Rudolff ne s'imposa donc pas immédiatement. Mais on la trouvera chez Stevin et Descartes et elle se généralisera avec Wallis et d'Alembert.
Ci-contre, la réédition par
Stifel, en allemand gothique, de la Coss de
Rudolff en 1553.
Le traité est téléchargeable, Université de Bielefeld,
Allemagne.
→
➔
L'appellation
racine
nous a été transmise par Al-Khwarizmi et symbolisée
par Al-Qalasadi au moyen du J arabe :
,
première lettre (jê) du mot jêdr signifiant racine,
base, placée au-dessus du nombre :
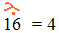
La racine carrée d'un nombre positif
x est le nombre
positif
y tel
que y2 = x. Elle exprime la mesure y du côté d'un carré dont l'aire
est x. La racine carrée de
16 est √16 = 4 car 42 = 4
× 4 = 16. Le nombre négatif - 4 est
l'opposé de la racine
carrée de 16.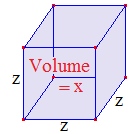
La racine cubique
d'un nombre x positif est est le nombre positif z dont le cube est x : z3
= x. On note z =
. Elle
exprime la mesure z du côté d'un cube dont le volume est x. La racine
cubique de 64 est 4. On peut dans là donner un sens au cas x < 0 car le cube
de x garde le signe de x :
(- 4) × (- 4) × (- 4) = + 16 × (- 4) = - 64.
» Newton , Parabole , Parabole cubique , Racines n-èmes
∗∗∗
| Racine carrée (auto-évaluation : propriétés opératoires de la racine carrée) |
| Construction de la racine carrée d'un nombre |
| Spirale de Théodore de Cyrène pour la construction de √n (n entier) |
! Collégiens, attention au vocabulaire :
Le concept de racine carrée a été défini et étudié dans l'Antiquité à une époque où celui de nombre négatif n'était pas encore à l'ordre du jour... Raison pour laquelle le nombre - 4 n'est pas, arithmétiquement et historiquement, une racine carrée de 16.
L'avènement des nombres complexes et le résultat selon lequel tout nombre complexe non nul admet n racines n-èmes, autorise à énoncer que dans l'ensemble C des nombres complexes, 16 possède deux racines carrées opposées qui sont 4 et - 4. Le nombre 4 étant la racine carrée arithmétique de 16.
Dans l'ensemble des nombres réels :
l'équation x2 = 16 possède deux solutions, à savoir + 4 (ou simplement 4) et - 4.
l'équation x2 = 2 possède deux solutions, à savoir √2 et - √2 et on pourra écrire x = ± √2.
|
Radical et radicande : |
Dans une écriture de la forme :
est
le radical (du latin radix,
radicis = racine). f(x) est le
radicande, qui semble apparaître plus
tardivement.
Cardan