
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Approximation d'une racine n-ème | Extraction d'une racine carrée "à la main" |
 Également appelé Héron l'Ancien, Héron
d'Alexandrie fut un disciple de Ctésibius (vers 170-117 av. J.-C.), un des
grands mécaniciens (mécanicien au sens étymologique : du grec
mêkhanê = machine) de l'Antiquité à qui on attribue l'invention de la
pompe aspirante et foulante.
Également appelé Héron l'Ancien, Héron
d'Alexandrie fut un disciple de Ctésibius (vers 170-117 av. J.-C.), un des
grands mécaniciens (mécanicien au sens étymologique : du grec
mêkhanê = machine) de l'Antiquité à qui on attribue l'invention de la
pompe aspirante et foulante.
Héron mit en pratique, dans divers domaines, ses connaissances en géométrie et en physique issues d'Euclide et d'Archimède : architecture, optique, réalisation de diverses machines (fontaines, machines à vent et à vapeur) et instruments de mesures géodésiques et astronomiques, comme la dioptre, ancêtre du théodolite (» réf.2), permettant les relevés d'angles dans des plans horizontaux ou verticaux et l'odomètre (hodos = route, metron = mesure) permettant de calculer les distances parcourues et dont le principe conduit au compteur kilométrique des bicyclettes indiquant également la vitesse instantanée.
Dans son Catoptrique, il expose le principe géométrique des lois de la réflexion basé sur un principe de moindre action selon lequel la lumière suit toujours le chemin le plus court.
Grandes inventions des grecs de l'Antiquité (sur Dailymotion) : »
En mathématiques, ses recherches et résultats sont réunis dans un important traité : Metrica (Les métriques, retrouvé à Constantinople en 1896). On y trouve en particulier l'aire A d'un triangle de côtés a, b et c, utilisant le demi-périmètre p = (a + b + c)/2 du triangle :
 (f)
(f)
formule qu'on lui attribue généralement, mais déjà prouvée par Archimède. On peut l'établir par un artifice trigonométrique utilisant la formule d'Al-Kashi et celle de l'aire du triangle : A = ½bc.sin^BAC.
Brahmagupta et le cas du quadrilatère : » Aire du triangle et quadrature : » ∗∗∗ Aire du triangle podaire
Problème de Héron d'Alexandrie :
Dans la tradition arithmétique pythagoricienne du "tout entier", Héron s'intéressa aux triangles d'aire entière dont les côtés sont mesurés par des entiers consécutifs. Outre le cas élémentaire du triangle rectangle égyptien de côtés 3, 4, 5, d'aire 6 ("moitié" d'un rectangle 3 × 4), on a les triplets (4, 13, 15, (5, 12, 13), (13, 14, 15), (51,52,53), ...
Notons a - 1, a, a + 1 les mesures consécutives des trois côtés, a désignant un entier naturel. Le demi-périmètre est p = 3a/2 et la formule (f) de Héron, exprimée ci-dessus fournit :

Multiplions les deux membres par 4 et élevons au carré :
16A2 = 3a2(a2 - 4) (1)
 Si a est impair, son
carré l'est aussi, ainsi que a2 - 4 et 16 ne
peut alors pas diviser 3a2(a2
- 4). Donc a est pair : posons a = 2x et remplaçons dans (1) ci-dessus; il vient
:
Si a est impair, son
carré l'est aussi, ainsi que a2 - 4 et 16 ne
peut alors pas diviser 3a2(a2
- 4). Donc a est pair : posons a = 2x et remplaçons dans (1) ci-dessus; il vient
:
A2 = 3x2(x2 - 1) (2)
Or si h désigne la hauteur associée au côté de mesure a, on a A = ah/2 = xh. Ce qui montre que h entier. Remplaçons dans (2) en simplifiant par x2 :
h2 = 3(x2 - 1)
Si le carré de h est un multiple de 3, alors h également (car h et h2 admettent les mêmes diviseurs premiers). Posons h = 3y, on obtient une équation de Pell-Fermat :
x2 - 3y2 = 1 , a = 2x
Une belle et complète solution de ce problème est proposé sur le site de la MAA (» réf.1). On pourra aussi résoudre cette équation au moyen du programme JavaScript sur la page consacrée à John Pell (1611-1685), fournissant (x,y) = (2,1), (7,4), (26,15), ...
| Calcul d'une valeur approchée de la racine carrée, cubique ou n-ème : |
On attribue à Héron une formule récurrente d'approximation de la racine carrée d'un nombre N, mais qui était déjà connu des Babyloniens, 300 à 400 années avant et s'écrivant de nos jours, au moyen des suites numériques :

L'algorithme de Héron est strictement équivalent à la formule d'approximation de Newton, dite des tangentes, appliquée à la fonction f(x) = x2 - N. C'est une méthode d'approximations successives relevant du théorème du point fixe.
Programmation de l'algorithme : en JavaScript : » | sur Tableur : »
Généralisation :
Notons que l'algorithme de Héron peut se généraliser au calcul d'une racine p-ème (cubique en particulier) en posant :

Toutefois, l'efficacité de la méthode diminue lorsque p augmente. On lui préférera la méthode de Newton appliquée à la fonction f(x) = xp - N fournissant la récurrence : rn+1 = [(p - 1)rn + N/rnp-1]/p soit, pour n = 3 (racine cubique) :
En posant rn+1 = h(rn), on a :
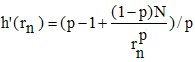
Au voisinage de la racine p-ème, le rapport N/rnp vaut sensiblement 1, ce qui permet d'affirmer que la fonction dérivée de h est, en valeur absolue, strictement inférieure à 1 : la convergence est assurée en vertu du théorème du point fixe.
|
Programmation de la méthode en JavaScript : |
Ce petit programme JavaScript calcule la racine cubique par les deux formules indiquées. Pour n = 27, dont la racine cubique est 3, le programme fournit en10 itérations :
La seconde formule converge beaucoup plus rapidement.
|
Algorithme de l'extraction de la racine carrée enseignée autrefois à l'école : |
poser une division, placer N "en dividende";
découper le nombre N en tranches de deux chiffres à partir de la droite;
prendre la racine carrée R du plus grand carré contenu dans la 1ère tranche (de gauche);
inscrire R à droite "en diviseur";
prendre la carré de R, le soustraire à la tranche; placez le résultat S sous la tranche;
abaisser la tranche suivante à la droite de S : on obtient un nombre D;
doubler la racine et la placer "en quotient" Q;
placer à droite de Q le plus grand chiffre u possible de sorte que le nombre obtenu multiplié par u n'excède pas D;
placer u à droite de R : on obtient la nouvelle valeur approchée de R;
poursuivre l'algorithme en reprenant au point n°6. Ne pas oublier la virgule lorsqu'on abaisse des tranches nulles 00.

Étude complète de cet algorithme sur la page d'Al-Banna : »
➔ Pour en savoir plus :
The Brahmagupta Triangles, par Ray Beauregard et E. R. Suryanarayan sur le
site de la MAA :
http://www.maa.org/sites/default/files/pdf/mathdl/CMJ/methodoflastresort.pdf
Sur le site L'Antiquité grecque et latine du Moyen Âge : http://remacle.org/bloodwolf/erudits/heron/dioptre.htm