
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
(théorème de Van Aubel) » Triangle de Napoléon |
i Peu d'infos sur H. van Aubel, professeur de mathématiques à l'Athénée royal d'Anvers (Belgique). Le résultat ci-dessous, limité au cas du quadrilatère, intitulé Note concernant les centres de carrés construits sur les côtés d'un polygone quelconque, apparaît dans le journal Nouvelle correspondance mathématique de Catalan, année 1878, tome 4, pages 40-44 (» réf.1).
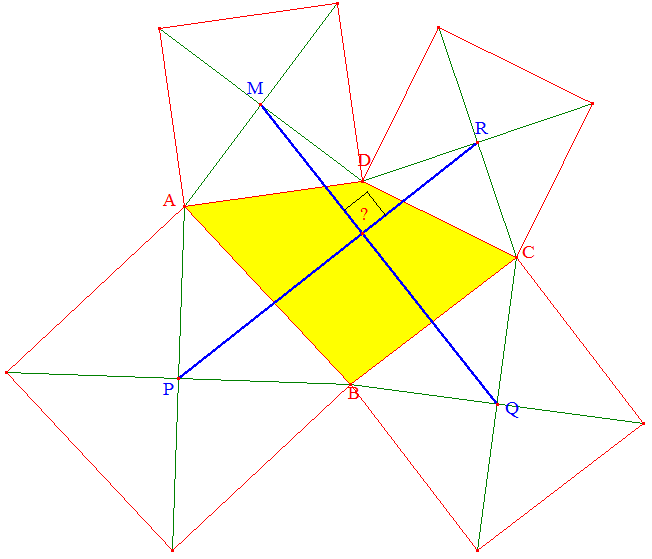
On considère un quadrilatère ABCD. On construit sur ses côtés, et extérieurement, les quatre carrés ci-dessous. On trace les diagonales de chaque carré.
Prouver, en passant dans le plan complexe, que les segments [MQ] et [PR] sont perpendiculaires et de même mesure

Si votre navigateur accepte les applets
Java (»
extension CheerpJ![]() ) :
) :
Vous pouvez déplacer A, B , C et D
»
Sous Java,
➔ Pas de panique ! la preuve de ce résultat est triviale au moyen des rotations si l'on se penche tout d'abord sur le cas triangulaire faisant elle-même appel à une variante plus simple encore... :
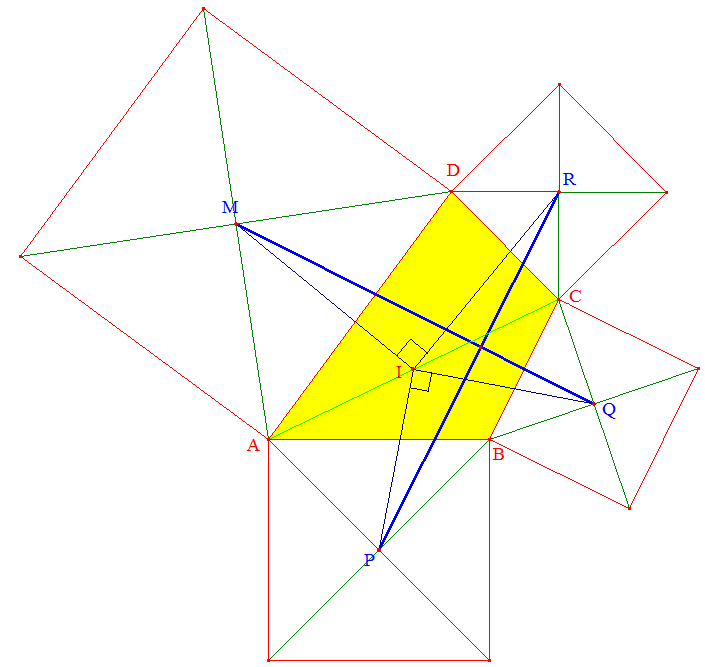
Montrer donc d'abord en observant la figure ci-dessous que ^MIR = ^PIQ = 90° et étudier la rotation de centre I qui transforme R en M...
➔ Pour en savoir plus :