ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

TORRICELLI Evangelista, italien, 1608-1647

Evangelista étudia auprès des jésuites à Faenza, sa ville natale, puis à Rome où il rencontra Galilée dont il devient un disciple et ami. Il s'établit à Florence en 1641, auprès de Galilée auquel il succède en tant que professeur de mathématiques, à sa mort en 1642.

Spécialiste en hydrostatique, son nom évoque surtout les recherches sur la pression atmosphérique qu'il met en évidence en 1643 : des fontainiers de Florence s'étaient adressé à Galilée suite à leur incapacité à faire jaillir l'eau des fontaines à plus de 32 pieds (soit environ 9,80 m). Et c'est Torricelli qui trouva l'explication et sera, cette année là, l'inventeur du baromètre à mercure portant son nom. L'ensemble de ces travaux fut publié en 1644 sous le titre De motu gravium naturaliter accelerato.

En mathématiques, il améliora sensiblement la méthode ardue, voire embrouillée, des indivisibles de Cavalieri, première approche du calcul intégral "moderne". Ses résultats mathématiques et physiques furent souvent publiés tardivement eu égard à leurs découvertes, ce qui lui posa de nombreuses querelles de paternité à une époque où la recherche scientifique s'amplifiait dans toute l'Europe.

»  Leibniz , Ceva , Newton , Riemann

En 1644, il publie son Opera geometrica, décrivant une méthode de construction des tangentes aux courbes (appelées "touchantes" à l'époque) et précisant l'aire de la cycloïde (3πr2, r désignant le rayon du cercle roulant), ce qui engendra une grave querelle de paternité avec Roberval qui avait déjà obtenu ce résultat en 1638 : cette année là, Mersenne, qui correspondait régulièrement avec Galilée, lui apprend le résultat. Ce dernier le communique à ses élèves, dont Torricelli... Débute alors des correspondances enflammées en termes de reconnaissance de paternité. Il meurt trois ans plus tard de la typhoïde. Il n'avait que 39 ans.

Le solide hyperbolique aigu, également appelé trompette de Torricelli :

En 1641, l'année de son installation à Florence, Torricelli découvre, par la méthode d'exhaustion et à son grand étonnement, un volume fini en forme de trompette de longueur infinie dont la surface est elle-même infinie qu'il baptise solide hyperbolique aigu : cette découverte relayée par Mersenne stupéfia la communauté mathématique et philosophique de l'époque, dont Pascal et Descartes, relativement à la notion d'infini.

En notations et calcul modernes, considérons le volume engendré par la rotation d'un arc d'hyperbole équilatère x→y = 1/x autour de l'axe des abscisses et s'étalant de 1 à l'infini.

Le volume de la "trompette" se calcule facilement en tant que solide de révolution. Il est effectivement fini :

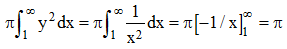
Qu'en est-il de la surface qui la délimite ? Considérons une tranche de la trompette d'épaisseur infinitésimale dx, définie dans l'intervalle [x - dx, x]. L'aire du cylindre ainsi défini, coloré en orange sur la figue de droite, a pour aire latérale dA = 2πy × dx = 2π/x × dx. Par conséquent, l'aire latérale A de la trompette est supérieure à :

» La trompette de Torricelli est également appelé trompette romaine ou encore trompette de (l'ange) Gabriel. On la trouve en effet sous une forme très semblable dans des représentations allégoriques chrétiennes et romaines, comme à Rome sur un bas relief de l'arc de Titus (81 après J.-C.) commémorant sa victoire sur les juifs :


Source photo : université de Bluffton, Caroline du Sud, USA : http://www.bluffton.edu/~sullivanm/titus/titus.html

Point de Torricelli, également dit de Fermat ou de Fermat-Torricelli :

Dans un triangle dont les mesures des trois angles sont inférieures à 120°, il s'agit du point minimisant la distance MA + MB + MC.

La recherche géométrique de ce point se rencontre souvent sous l'appellation problème de Fermat car ce dernier le proposa à Torricelli vers 1655. De l'unique point M minimisant MA + MB + MC, on voit les côtés du triangle ABC sous un angle de 120°. Ce fut Viviani, un élève de Torricelli qui publia la solution de son maître en 1659.

Étude mécanique du point de Fermat-Torricelli :  »

 ➔   Pour en savoir plus :

Roberval   Pell 
© Serge Mehl - www.chronomath.com