
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Galilée, bien avant l'EDF..., fut sans doute le premier à s'intéresser à la chaînette qu'il prit pour un arc de parabole. Un demi-siècle plus tard, Jean Bernoulli, Huygens et Leibniz trouvèrent (indépendamment) en réponse au défi lancé par Jakob Bernoulli, sa véritable nature en 1691 : engendrée par un cosinus hyperbolique.

Considérons un câble homogène, flexible, attaché en deux points A et B. Dans sa position d'équilibre, le câble pend dans un plan vertical et semble prendre une forme parabolique. En fait, pas vraiment...
➔ Dans toute la suite l'écriture en italique gras désignera un vecteur :
Créons dans ce plan un repère orthonormé (O, i, j), où O désigne le point le plus bas du câble et notons g le champ de pesanteur à son endroit.

Nous admettons ici un principe de statique :
la tension T qui s'exerce en un point M(x,y) du câble est portée par la tangente en M
Appelons To la tension au point O faisant échec à la tension en M de sorte que la portion de câble [OM] de longueur L, soumise à son poids au point G , soit en équilibre au sens statique : c'est dire que si µ désigne la densité linéaire du câble, nous avons la relation vectorielle :
Projetons sur les axes de coordonnées en notant â l'angle ^(i, T). On a les décompositions suivantes :
On peut alors écrire le système :
| (s) | ||
T
||.cos â - || To || = 0 || T ||.sin â - µL.|| g || = 0 |

Téléphérique du
Pic du Midi
de Bigorre : en l'absence de charge, entre deux
pylônes,
le câble accuse une certaine flèche et épouse la
forme d'une chaînette →
Afin de simplifier les écritures, nous
posons µ.|| g || = p et k = || To
||/p.
Il vient alors en éliminant || T
|| dans (s)
:
Pour obtenir une relation entre les coordonnées x et y de M sous la forme cartésienne y = f(x), nous allons différentier l'équation (e1) :
Considérons alors le point M'(x+dx,y+dy) du câble. L'équation (e2) caractérise l'équilibre de la portion de câble [MM'] de longueur infinitésimale dL au voisinage de M(x,y).
Par symétrie, on peut supposer dx > 0. Dans ces conditions, puisque T dirige la tangente en M : tan â = dy/dx. En posant dy/dx = y', vu que dL2 = dx2 + dy2, on obtient :
Mais dy'/dx n'est autre que y" (dérivée seconde de y par rapport à x) : nous sommes donc en présence d'une équation différentielle du second ordre :
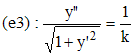
qu'il sera aisé de ramener au premier ordre en posant u = y'. Le membre de gauche est facilement intégrable :
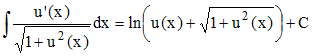
Intégrons donc (e3) et passons à l'exponentielle, en remarquant qu'en x = 0 on a y' = 0 :
C'est dire que :
En remarquant enfin qu'en x = 0 on a aussi y = 0, la solution de (e4), donc de (e3) et de notre problème sera :
avec X = x , Y = y + k, cosh désignant la fonction cosinus hyperbolique.

➔ Le choix particulier de l'origine que nous avons fait dans ce calcul évite l'intervention des coordonnées de A et B. Ces dernières interviennent au niveau du calcul des constantes d'intégration. Le cas général fournit un résultat de la forme :

et conduit sans peine au calcul des constantes C1 et C2 en exprimant que la courbe passe par A et B.
| Applications : |
♦ La chaînette est d'une importance capitale car elle permet de calculer les flèches (c'est à dire la distance de l'arc à la corde) à donner aux câbles suspendus afin que les tensions aux points d'accroche ne soient pas excessives (comme à gauche sur des pylônes EDF). En effet, dès que l'on cherche à tendre par trop un câble entre deux pylônes, les tensions deviennent considérables.

♦ Dans le cas des lignes de chemins de fer électrifiées, on remédie à la flèche rédhibitoire par un câble porteur principal de la caténaire (câble conduisant le courant alimentant la locomotrice, du latin catena = chaîne) : le câble supérieur (ci-dessous à droite) subit une flèche acceptée, ce qui diminue les tensions entre les pylônes.

La caténaire reste ainsi bien linéaire grâce aux accroches auxiliaires multiples à un câble auxiliaire. D'ailleurs, l'ancien nom de la chaînette fut précisément la caténaire, nom qui lui est resté en anglais (catenary).
♦ Ci-dessous, les câbles soutenant les tabliers de ponts suspendus ont une forme parabolique apparaissant comme approximation d'une chaînette : le poids du câble étant très faible comparé à celui du tablier, la composante verticale de son poids (qui s'applique sur les piliers verticaux) peut être négligée dans le calcul précédent.

Pont sur le petit Rhône - Languedoc
Par suite dans le calcul de µL.g de la théorie ci-dessus, avec dL2 = dx2 + dy2, on peut écrire sensiblement dL = dx, ce qui conduit à l'équation très simple : dy' = dx/k, c'est à dire y" = 1/k.
Finalement y = ½x2/k + C1x + C2 : c'est l'équation d'une parabole. Les deux "moitiés" de parabole, fixées sur les rives, équilibrent les poussées sur les deux piles du pont.
➔ Notons enfin que la chaînette est la roulette du foyer d'une parabole, autrement dit le lieu de son foyer lorsqu'elle roule sans glisser, sur une droite :