ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Ovales
de Cassini |
On donne dans un plan deux points F1 et F2. k désignant un nombre réel positif non nul, un ovale de Cassini est l'ensembles des points M du plan vérifiant :
On pose F1F2 = 2a. L'équation cartésienne d'une telle courbe est obtenue en élevant au carré :
Elle montre qu'un ovale de Cassini est une courbe algébrique de degré 4 : quartique. C'est une quartique bicirculaire puisque cette équation peut s'écrire :
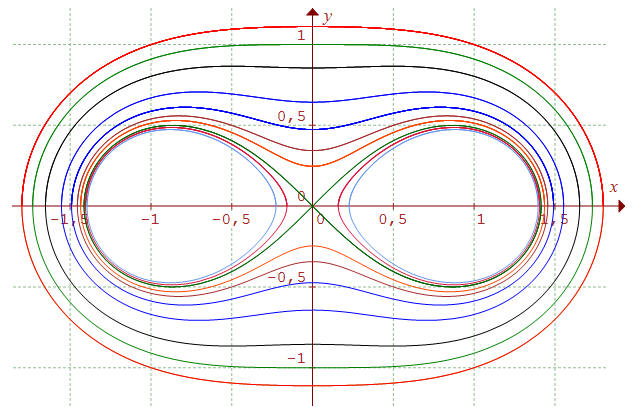
Mais une telle forme n'est guère pratique pour notre étude. Plaçons-nous en coordonnées polaires. Le pôle sera le milieu O de [F1F2]. L'axe polaire étant orienté en direction de F2.
On note M(r,t) un point du plan, t est exprimé en radians. Dans ces conditions, selon la formule d'Al Kashi :
Élevons au carré et reportons dans l'équation de définition. Une équation bicarrée en r conduit à :
Si k < a, on obtient deux courbes
fermées symétriques par rapport à l'axe des
ordonnées. Ci-dessous : k < a : a = 3, k = 2. Les foyers
sont en F1(-3;0) et F2(3;0).
Si
a et k sont assez voisins, on obtient ceci (a = 3 et k = 2,97)
:
Si k = a, on obtient
r2 = 0 pour tout t (que nous rejetons) ou bien
r2 = 2a2cos 2t : c'est une lemniscate.
Ci-dessous, k = a = 2 :
Lemniscate
de Bernoulli : 
Si k > a, la quantité sous le
radical est toujours positive. On obtient un seul ovale dont
l'équation se réduit à :
Si
k est "plus voisin" de a : a = 2, k = 5/2 , on obtient ceci
:
Ovale de Descartes
Tore
et ovales de Cassini :
Courbes
cycliques :
