ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 GULDIN Paul,
suisse, 1577-1643 |
Issu d'une famille juive, Habakuk Guldin fut élevé dans le protestantisme avant de se convertir au catholicisme et prendre le prénom de Paul. Orfèvre de formation, il entre dans la compagnie de Jésus et découvre les mathématiques. Guldin enseigna à Rome et en l'université de Graz (Autriche), nouvellement fondée (elle vit le jour en 1586).
Il est principalement connu pour ses formules relatives aux calculs d'aires et de volumes dans son traité Centrobaryca seu de Centro gravitatis (1635/1640), où il fait intervenir le centre de gravité. C'est à Cavalieri que l'on devra la démonstration de ces énoncés. A noter que Pappus d'Alexandrie avait énoncé le premier théorème énoncé ci-dessous treize siècles auparavant.
| Deux théorèmes de Guldin : |
1. Si
D
désigne un domaine plan d'aire
A, de
centre de gravité G, le volume V engendré par la
rotation de D autour d'un axe Δ situé dans son plan et ne le coupant pas est donné
par la formule :
V = 2πA × GH , où H est le projeté orthogonal de G sur Δ
En d'autres termes :
le volume engendré par D est égal au produit de son aire par la longueur du cercle décrit par son centre de gravité.
Calcul de la position du centre de gravité d'un solide : »
2. Si (C) désigne un arc de courbe plane de longueur L, de centre de gravité G, tournant autour d'un axe Δ ne la rencontrant pas, la surface engendrée par (C) a pour aire :
A
= 2πGH × L,
où H est le projeté orthogonal de G sur
Δ
➔
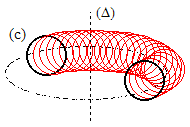
Par
exemple, l'aire du
tore
engendré par la rotation
d'un cercle (c) de rayon r dont le centre est situé à
la distance a de l'axe (Δ) est
4π2ra.
Son volume est 2aπ2r2.
Volume de révolution, cas de la pyramide, du cône, de la sphère : »
∗∗∗
a) Montrer, en utilisant le
premier théorème de Guldin que le centre de gravité d'un demi disque de
rayon R est situé
sur son axe de symétrie à la distance d = 4R /
3π de son centre.
»
méthode par intégration
»
on utilisera le fait que
le volume engendré est ici une boule
de volume 4/3πR3
= 2π
x
πR2/2
x
d
a) Montrer, en utilisant le
second théorème de Guldin que le centre de gravité d'un demi cercle de
rayon R est situé
sur son axe de symétrie à la distance 2R /
π de son centre.
»
l'aire engendrée est ici une
sphère
d'aire 4πR2
= 2πd
x
πR
c) Calculer le volume
V
engendré par la rotation d'une demi arche de sinusoïde sur l'intervalle [0,π/2].
Rép : V = π2/4
En déduire que l'ordonnée du centre de gravité de la surface délimitée par cette
demi arche est égale à π/8.
Bachet