ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
 
Fibration de la sphère
S3 de l'espace quadridimensionnel
(fibration de Hopf) |
Dans un article écrit en 1930, intitulé Über die Abbildungen der dreidimensionalen Sphäre auf die Kugelfläche (à propos du mappage de la sphère tridimensionnelle sur la surface sphérique) paru dans les Mathematiche Annalen de Clebsch et C. Neumann en 1931, le mathématicien allemand Heinz Hopf (1894-1971) nous montre à quoi devrait ressembler une sphère en dimension 4 par le biais du concept d'espace fibré.
On ne manquera pas de visionner les superbes
vidéos
d'Étienne Ghys, J. Leys & A. Alvarez décrivant cette fibration (»
réf.1) au moyen de la
projection stéréographique. L'approche ci-dessous se veut
élémentaire tout en évitant, je l'espère, des imprécisions néfastes. Elle laisse aux spécialistes de ce difficile sujet les arguments et les preuves
relevant de la topologie algébrique,
homotopie en particulier.
Le lecteur intéressé par ce très beau sujet, pourra consulter les liens universitaires proposés in fine le décrivant dans son aspect général beaucoup plus théorique et, par là, plus rigoureux, comme l'étude par le biais des quaternions unitaires, remarquablement exposée, comme celle de David Lyons (» réf.6) ou encore celle du collectif H. P. de Saint-Gervais (site Analysis situs » réf.7a -7b).
I - L'espace euclidien R4 de dimension 4 est muni de sa base canonique. Suivant le contexte, on le verra comme un espace vectoriel ou affine; dans ce dernier cas, on pourra nommer une origine des coordonnées pour signifier le point de coordonnées nulles dans R4 ou dans un de ses sous-espaces; elle n'a que peu d'importance : on s'intéresse aux propriétés métriques et topologiques des variétés rencontrées.
L'hypersphère de rayon 1, notée S3, objet de cette étude, sera ici l'ensemble des points de R4 dont le quadruplet de coordonnées (x,y,u,v) vérifie l'équation :
x2 + y2 + u2 + v2 = 1
➔ On parle de S3, et non pas S4, pour rappeler que cette sphère ne possède que 3 coordonnées indépendantes. Elle est la surface de la boule B4 : x2 + y2 + u2 + v2 ≤ 1. La sphère unité de notre espace euclidien usuel R3 de dimension 3 est notée S2 : d'équation x2 + y2 + z2 = 1, elle ne possède que deux coordonnées indépendantes. Le cercle unité de R2 est noté S1 : d'équation x2 + y2 = 1, il ne possède qu'une coordonnée indépendante.
Quand on parlera de S1 par la suite, on entendra un plongement de ce dernier dans l'espace R3 ou R4. Il pourra aussi s'agir d'une variété fermée qui lui est homéomorphe.
Produit scalaire et distance : » Espaces métriques : »
II - L'application de Hopf : considérons l'application h1 (h comme Hopf) qui à tout (x,y,u,v) de S3 associe le triplet (X,Y,Z) de R3 défini par :
X = 2(xu + yv) , Y = 2(yu - xv) , Z = (x2 + y2) - (u2 + v2)
Un calcul élémentaire conduit à : X2 + Y2 + Z2 = (x2 + y2 + u2 + v2)2 = 12 = 1 : h1 applique donc S3 dans S2.
h1 : S3 → S2 , h1(x,y,u,v) = (2(xu + yv) , 2(yu - xv) , (x2 + y2) - (u2 + v2)) (h1)
i Un point de S3 s'interprète comme un quaternion unitaire q. Quitte à échanger les rôles de u et v, au moyen des quaternions l'application de Hopf peut s'écrire h(q) = q×i×q-1 = q×i×q (car q étant unitaire q-1 = q).
III - S3 vue comme variété de C2 et application de Hopf : identifions maintenant R4 à H, espace vectoriel des quaternions d'Hamilton de dimension 4 sur R. Tout quaternion est de la forme q = x1 + yi + uj + vk, avec 1(1,0,0,0), i(0,1,0,0), j(0,0,1,0), k(0,0,0,1). Vu que ij = k (au sens du produit des quaternions), on peut écrire q = (x + yi)1 + (u + vi)j, ce qui nous amène à identifier H et R4 à C2, espace vectoriel complexe de dimension 2 sur C, de base orthonormée (1,j) avec 1(1,0,0,0) et j(0,0,1,0).
Dans cette interprétation de l'espace quadridimensionnel on se retrouve à deux dimensions et les coordonnées complexes (z1,z2) d'un point de C2 sont de la forme z1 = x + yi et z2 = u + vi, décrivant deux "axes" orthogonaux caractérisés l'un par z1 = 0, l'autre par z2 = 0, qui ne sont autres que deux plans d'Argand-Cauchy. En effet, par exemple, si z2 = 0, la 1ère coordonnée z1 = x + yi décrit C, dont l'interprétation est un plan euclidien. On reviendra plus en détail sur ce résultat étonnant dans le paragraphe V.
Représentation 3D de C2
- vidéo d'Étienne Ghys, J. Leys
& A. Alvarez
(réf. 1b)
Notons dès à présent :
Dans l'espace C2, l'équation x2 + y2 + u2 + v2 = 1 de la sphère unité S3 devient |z1|2 + |z2|2 = 1, (z1,z2) ∈ C2.
Dans ce contexte, considérons la sphère S2 en tant qu'ensemble de points (X + iY, Z) de C × R vérifiant X2 + Y2 + Z2 = 1. Une seconde formulation h2 de l'application de Hopf se définit alors de S3 dans S2 par X + iY = 2(xu + yv) + 2i(yu - xv) = 2(x + iy)(u - iv) = 2z1z2 et Z = |z1|2 - |z2|2, donc par :
h2 : S3 → S2 , h2(z1,z2) = (2z1z2, |z1|2 - |z2|2) (h2)
➔ Vu que z2 = z2, on peut vérifier facilement que |4z1z2|2 + ( |z1|2 - |z2|2)2 = 1.
IV - L'application de Hopf "vue" par projection stéréographique : la sphère unité "usuelle" S2 de R3 peut être identifiée à C∪{∞}, dite sphère de Riemann, par projection stéréographique s de pôle N(0,0,1), "pôle nord", sur son plan équatorial (E) identifié à C :
Tout point M(X,Y,Z) de la sphère S2 autre que N s'identifie ainsi à un nombre complexe α de C. Le pôle N a pour projection le point à l'infini. Dans ces conditions, par la projection stéréographique s, M(X,Y,Z) distinct de N aura pour image :
s(M) = α = (X + iY)/(1 - Z) » expr. analytique proj. stéréo.
Selon (h2), on a :
X + iY = 2z1z2 , Z = |z1|2 - |z2|2
donc α = 2z1z2/(1 - |z1|2 + |z2|2) = 2z1z2/2|z2|2 car |z1|2 + |z2|2 = 1. Mais |z2|2 = z2z2. D'où cette formulation remarquablement simple de l'application de Hopf pour tout (z1,z2) de C2, z2 non nul :
h3 = s o h2 : S3 → S2 , h3 (z1,z2) = z1/z2 (h3)
➔ Par changement d'orientation d'un axe, on peut obtenir un résultat différent mais équivalent (comme le conjugué z1/z2). Et par projection stéréographique de pôle sud, on obtiendrait le résultat inverse z2/z1.
V - La notion de fibration de S3 :
De façon simplifiée, la définition d'un espace fibré peut être la suivante : étant donnés trois espaces topologiques E, F, B et p une application continue surjective de E dans B (souvent appelée projection), on dit que E est un espace fibré (» Whitney) lorsque pour tout x de B, l'image réciproque de x, notée p-1(x) appelée fibre au-dessus de x, est homéomorphe à F. Lorsque E, F et B sont des variétés différentielles de même classe, on parle de fibration lorsque p-1(x) est difféomorphe à F (homéomorphie différentiable).
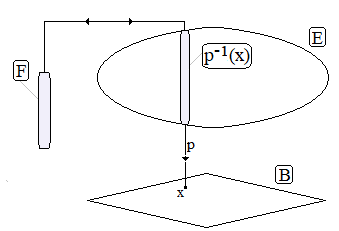
Intuitivement
: étant donné un espace E (espace total) dont
on cherche à connaître les propriétés topologiques et différentielles, on lui
associe un espace "connu" B (la base) au
moyen d'une application convenable p (la projection)
telle que chaque image réciproque des points de B soient homéomorphes à un même
espace F (la fibre). En tant que réunion
disjointe des p-1(x), E
s'identifie à une trame ("très serrée", ensemble de ses fibres), susceptible,
comme dans le cas présent, de nous renseigner sur son aspect géométrique.
➔ Dans le cas présent, E = S3 , B = S2, p est l'application de Hopf sous forme h3 = s o h2 et la fibre, comme on va le voir, sera constituée de cercles S1.
VI - Droites "complexes" de C2 et nature des fibres : considérons l'application de Hopf sous sa forme (h3) du §4. La fibre au-dessus de α = z1/z2 à savoir h3-1(α), ensemble des antécédents de α par h3 vérifie dans S3 :
z1|2 + |z2|2 = 1 , z1 = αz2 (z12)
♦ Dans C2, une équation du type z1= αz2, avec α complexe, n'exprime pas à proprement parler une "colinéarité" de z1 et z2. On peut cependant écrire (z1,z2) = (αz2,z2) = z2(α,1), z2 décrivant C ce qui définit une droite vectorielle de C2, en tant que sous-espace de dimension 1 sur C engendré (α,1). On peut aussi parler de droite complexe de C2 passant par l'origine. De même pour les cas z1= 0, cas particulier α = 0, engendrée par (0,1) et z2= 0, droite complexe engendrée par (0,1), axes de l'espace C2.
Ces droites sont ainsi homéomorphes à C et s'interprètent donc comme un plan d'Argand-Cauchy. De tels plans, qui n'ont que l'origine en commun, rencontrent S3 selon le système d'équations (z12) conduisant à |z2| = 1/(1 + |α|2)1/2
L'ensemble h3-1(α) des antécédents de α par h3 est donc un cercle de S3 de la droite complexe z1= αz2.
♦
h3-1(0)
est la fibre au-dessus de l'origine de S2,
image du pôle sud S par
s
lorsque α
= 0 : cercle |z2|
= 1 de la droite complexe z2
= 0.
♦
L'intersection
avec l'axe z2 = 0 correspond à α s'éloignant à l'infini (|α|
→ ∞) : z1 et z2 étant de module borné
vérifiant z1|2 + |z2|2
= 1, |z2| → 0 équivaut à z2 →
0 et |z1| → 1. Et cela permet de considérer h3-1(∞)
en tant que cercle de rayon unité de la droite complexe z2
= 0.
Il apparaît ainsi que
toute droite complexe de C2 ≡ R4
coupe la sphère S3
suivant un cercle S1.
S3 contient donc une infinité (non dénombrable) de cercles S1
dont elle est, en théorie, réunion.
Mais qu'en est-il de leur agencement ?
VII - Autrement dit, à quoi devrait ressembler S3 dans R4 ? :
Les cercles rencontrés ci-dessus sont les cercles de Hopf. Puisque situés sur des droites complexes n'ayant que l'origine en commun, ils n'ont aucun point commun dans S3. On peut montrer plus précisément que toute paire de cercles est liée : elle forme un entrelacs dit entrelac de Hopf. On consultera les pages 11-13 de Niles Johnson consacrées à ce résultat (» réf.6).
Entrelacs de deux cercles
Un
point de S2 décrit ci-dessus un parallèle de cote Z, 0 < Z < 1
- vidéo d'Étienne Ghys, J. Leys
& A. Alvarez
(réf. 1b)
Rappel : considérons ci-dessous le tore de révolution engendré par la rotation d'un cercle de centre A de rayon r autour d'un axe Oz situé dans son plan et ne le coupant pas (OA = a > r). Avec les notations de la figure ci-dessous, dans le repère orthonormé (O,x,y,z), une équation paramétrique de cette surface est alors x = (a + r.cos u)cos v , y = (a + r.cos u)sin v , z = r.sin u. Un point M du tore est ainsi caractérisé par sa position sur chacun des deux cercles au moyen du couple angulaire (u,v), u et v décrivant [0,2π]. On en déduit un résultat admis ici :
Le tore est topologiquement homéomorphe à S1 × S1
Considérons maintenant les parallèles de S2, ce sont des cercles parallèles à son plan équatorial (E) ≡ C. Ils sont caractérisés par la valeur constante de |α| = |z1/z2|. La cote Z d'un point M(X,Y,Z) situé sur un tel parallèle décrit l'intervalle réel ]-1,1[. La réunion de tous ces cercles lorsque Z varie n'est autre que S2 privée de N et S.
L'équation paramétrique de la sphère unité S2 peut s'écrire :
Pour tout Z = sin
t,
on a X + iY =
(cosθ
+ i sinθ)cost
= eiθcost,
θ décrivant [0,2π]; α = (X + iY)/(1 - Z) =
eiθcost/(1
- sint).
On en déduit
les équations des fibres au-dessus de chaque parallèle (pt)
:
|z1|2 + |z2|2 =
1 ,
|z1/z2|
= cost/(1 -
sint)
Ce système conduit à :
|z1| =
[(1 + sint)/2]1/2
, |z2| = [(1 - sint)/2]1/2
z1 et z2 parcourent donc des cercles sans
condition sur leurs arguments. Posons r1 = [(1 + sint)/2]1/2
et r2 = [(1 - sint)/2]1/2
on a :
h3-1(pt) = {(z1,z2) ∈ S3, |z1| = r1, |z2| = r2} ≡ S1 × S1
C'est dire que la fibre au-dessus de (pt) doit être interprété comme un tore.
En conclusion :
La sphère S3 peut donc s'imaginer comme une famille de tores imbriqués. Une conclusion cachant une "réalité" plus complexe, en choisissant des cercles de Villarceau pour générer les tores (» réf. 1b, 2, 7b).
Cercles de Villarceau - Vidéo d'Étienne Ghys, J. Leys
& A. Alvarez
(réf. 1b)
Vidéo d'Étienne Ghys, J. Leys
& A. Alvarez
(réf. 1b)
Autre vision du
cœur de l'hypersphère S3 de R4...
Source : Niles Johnson (Ohio
State University) :
https://www.youtube.com/watch?v=AKotMPGFJYk
Quaternions et fibration de Hopf - sur
Analysis Situs (réf.7b)
➔ Pour en savoir plus :
vidéos d'Étienne Ghys, coproduction J. Leys & A. ALvarez, issues du site
dimensions-math.org, ch. 7 &
8,
http://dimensions-math.org/Dim_CH7.htm
1ère partie : fibration de Hopf :
https://www.youtube.com/watch?reload=9&v=I0FIWCWLptE
2è partie : (fibres toriques, lien avec les
cercles de Villarceau)
:
https://www.youtube.com/watch?v=F-9mpqAsg9ESur le site Analysis situs
du groupe Henri Paul de Saint Gervais :
a) Quaternions, rotations, fibrations :
http://analysis-situs.math.cnrs.fr/Quaternions-rotations-fibrations.html
b) Explorer la sphère de dimension 3 par les quaternions, tores et
cercles de Villarceau :
https://www.youtube.com/watch?v=E-qbVQ8ygTc&feature=youtu.be
a) Über die Abbildungen der dreidimensionalen Sphäre auf die
Kugelfläche, par Heinz Hopf (Math. Annalen, Göttingen, 1930) :
https://gdz.sub.uni-goettingen.de/id/PPN235181684_0104?tify={%22pages%22:[641],%22view%22:%22info%22}
b) Voir aussi l'étude plus générale de H. Hopf (1935) :
Über die Abbildungen von Sphären auf Sphären niedrigerer Dimension :
http://matwbn.icm.edu.pl/ksiazki/fm/fm25/fm25135.pdf