
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


Normalien, Joseph Oesterlé obtint son doctorat à la faculté des sciences d'Orsay en 1977, sa thèse portait sur les opérateurs de Hecke, un sujet attaché à la théorie des formes modulaires au sein de la théorie analytique des nombres. Membre du groupe Bourbaki, professeur à la faculté des sciences de Paris (UMPC, Paris VI), Joseph Oesterlé dirigea l'Institut Henri Poincaré de 1994 à 1998.
i Erich Hecke (1887-1947) : mathématicien allemand, élève de Hilbert à Göttingen.
Suite à des échanges avec le mathématicien anglais David Masser (1985) relatifs à la conjecture de Taniyama-Weil (» ref.1), on doit en particulier à Joseph Oesterlé la formulation conjointe, en 1988, de la conjecture ABC, un sujet particulièrement ardu d'arithmétique (théorie additive des nombres) dont la preuve conduit en particulier à celle du "grand" théorème de Fermat, aujourd'hui théorème de Fermat-Wiles, de la conjecture de Mordell portant sur les courbes algébriques à coordonnées rationnelles ainsi qu'à l'infinitude des nombres premiers de Wieferich.
i David William Masser (1948-) : mathématicien anglais, élève d'Alan Baker à Cambridge (Royaume Uni). CV & publications : univ. Bâle
| La conjecture ABC : |
La conjecture d'Osterlé-Masser s'intéresse à la décomposition en produit de facteurs premiers des entiers naturels et exprime, grosso modo, que si A et B sont deux entiers possédant de nombreux diviseurs, alors il est peu probable que C = A + B possède cette même propriété. Mais comment formaliser cette assertion quelque peu floue ?...
Certains mathématiciens qualifient de riche un entier dont la décomposition en facteurs premiers admet au moins un facteur pk, p premier, k ≥ 2. Cette notion de richesse est très relative : 756 = 22 × 33 × 7 est riche et possède : 24 diviseurs; 800 = 25 × 52 est riche et possède 18 diviseurs. Leur somme 756 + 800 = 1556 = 22 × 389 est également riche mais ne possède que 6 diviseurs : la conjecture ABC s'applique ici mais mieux encore avec 18 = 32 × 2 et 25 = 52 tous deux riches alors que 18 + 25 = 43 est premier, donc pauvre...
Ce programme élémentaire calcule
le nombre de diviseurs d'un nombre
Vous pouvez entrer une somme d'entiers
naturels sans en faire la somme. L'ordinateur la fera pour vous.
Tous les diviseurs et leur somme : »
Le théorème de Fermat évoqué ci-dessus selon lequel il n'existe aucun c tel que an + bn = cn si n est supérieur à 2 est un exemple fameux confortant la conjecture. De même la somme de deux nombres puissants (entiers dont les exposants des facteurs premiers de sa décomposition sont au moins égaux à 2) est rarement un nombre puissant.
:-) Dans un propos mathématique, utiliser peu probable ou rarement n'est ni rigoureux, ni convaincant... Précisons :
Radical (ou noyau) d'un entier naturel :
On appelle radical d'un nombre entier naturel n la fonction arithmétique égale au produit de tous ses diviseurs premiers. Autrement dit, le radical de n est l'entier obtenu en réduisant à l'unité tous les exposants de sa décomposition en facteurs premiers :
Si n = p1α × p2β × ... × pkγ, son radical est rad(n) = p1 × p2 × ... × pk.
» Lien analogique : anneau produit Z/p1Z × Z/p2Z × ... × Z/pkZ
➔ Cette appellation radical n'est pas très heureuse. Elle n'a rien à voir avec la racine carrée de n à moins que tous les exposants de sa décomposition soient égaux à 2. Noter que l'application n → rad(n) n'est pas injective. Par exemple 23 × 32 = 72 et 22 × 33 = 108 ont même radical, à savoir 6. Certains mathématiciens préfèrent parler de noyau plutôt que de radical; d'autres anglo-saxons parlent de square-free part pour exprimer une écriture en produit de facteurs premiers sans aucun facteur carré (aucun facteur premier n'admet d'exposant de degré 2 au moins) : 72 contient deux facteurs carrés 22 contenu dans 23 et 32; sfp(72) = 2 × 3 = 6.
∗∗∗
Quelques propriétés
de la fonction radical :
Pour tout n de N, rad(n) ≤ n;;
Pour tout nombre n premier ou ne comportant aucun facteur carré, rad(n) = n;
Pour toute puissance n-ème non nulle d'un entier x, rad(xn) = rad(x);
Pour tous n et m de N premiers entre eux, rad(n × m) = rad(n) × rad(m) : mais cette fonction arithmétique n'apparaît que faiblement multiplicative en ce sens que si n et m ont des facteurs communs l'égalité précédente n'a généralement pas lieu. Par exemple : rad(216) = rad(18 × 12) = 6 ≠ rad(18) × rad(12) = 36.
» Lien analogique : fonction µ de Möbius , fonction indicatrice d'Euler
Richesse d'un nombre n :
On peut quantifier la richesse d'un nombre n, au sens évoqué ci-dessus, au moyen de son radical en définissant au moyen du nombre ρ défini par n = (Rad(n))ρ. Autrement dit :
ρ = ln(n)/ln(Rad(n))
En quelque sorte ρ est l'exposant "moyen" (généralement un nombre réel) auquel il faut élever tous les facteurs premiers de n afin d'égaler n.
Pour tout nombre premier, ρ = 1;
Pour toute puissance n-ème d'un nombre premier, ρ = n;
Pour tout nombre puissant (de la forme a2b3, a ≥ 1, b ≥ 1), on a ρ ≥ 2;
➔ Grace à l'usage des ordinateurs, les mathématiciens ont pu constater empiriquement que la richesse moyenne des entiers est de l'ordre de 1,06. Le graphique ci-dessous (» réf.2) exprime qu'en terme de richesse la très grande majorité des entiers se situe dans le bandeau rouge, donc ρ ≈ 1. Est déclaré riche tout entier de richesse au moins égal à 2. De tels nombres sont "rares" dans la distribution des entiers naturels (» réf.2&9) : c'est le cas de toute puissance n-ème, an si n ≥ 2, et il apparaît plus rare encore, toujours empiriquement, que la somme de deux nombres riches soit riche, donc qu'une égalité du type an + bn = cn se produise...
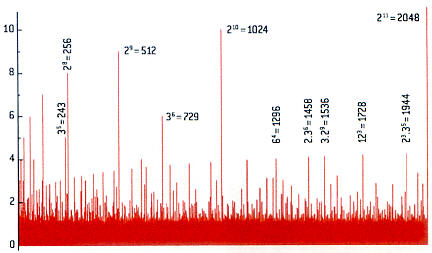
Illustration de la richesse des entiers sur l'intervalle
[2, 2048].
Source :
La conjecture ABC, par Gerhard Frey (Univ.
Duisburg-Essen)
in revue Pour la Science n°421 - Nov. 2012.
Conjecture ABC :
Pour tout ε > 0, il existe un réel dε
> 0 tel que si (A,B,C) est un triplet d'entiers relatifs premiers entre eux
vérifiant C =
A + B, alors : max(|A|, |B|, |C|) < dε ×
(![]() rad(ABC)
rad(ABC)![]() )1 + ε
)1 + ε
On peut exprimer plus particulièrement :
Pour tout ε > 0, il existe un réel dε
> 0 tel que si (A,B,C) est un triplet d'entiers naturels premiers entre eux
vérifiant C =
A + B, alors : C < dε ×
(![]() rad(ABC)
rad(ABC)![]() )1 + ε
)1 + ε
i Il existe de nombreuses formulations de la conjecture et des variantes dites faible et forte. Le choix ci-dessus est (en particulier) celui des références 1 à 4 que l'on pourra consulter in fine. Tout développement de ce difficile sujet ne saurait égaler la pertinence et la qualité pédagogique des exposés référencés in fine, à moins de s'en fortement inspirer... raison pour laquelle la parole est laissée aux spécialistes du sujet :
à commencer par Joseph Oesterlé dans son exposé Nouvelles approches du « théorème » de Fermat (1988, » réf.1).
Gerhard Frey, professeur à l'Institut de mathématiques de l'université Duisbug-Essen (Allemagne), développe la genèse de la conjecture dans un passionnant article de la revue Pour la science (novembre 2012, » réf.2).
E. Crouseilles & A. Lardeur sous la direction de Bernard le Stum, université de Rennes (2018, » réf.3) exposent diverses formulations de la conjecture ABC et ses conséquences (preuve du théorème de Fermat et de la conjecture de Mordell, avancées dans la conjecture d'Erdös-Woods et l'étude des nombres premiers de Wieferich).
Tom Wright, professeur à l'université de Caroline du sud, présente le sujet avec tant d'humour que de rigueur (» réf.4) avant de nous prouver que xn + yn = zn ne peut avoir lieu que si n est inférieur à 6.
Dans Beyond the last theorem (Au-delà du dernier théorème), Dorian Goldfeld de l'université Columbia, prix Cole 1987, s'intéresse au dernier théorème de Fermat en évoquant l'approche spécifique de Wiles, comparée à l'usage plus universel de la conjecture face aux équations diophantiennes si celle-ci venait à être prouvée.
Conjecture de Bieberbach : » Empilement de sphères : »
➔ Pour en savoir plus :
Nouvelles approches du « théorème » de Fermat
par Joseph Oesterlé (Séminaire bourbaki, 1988) :
http://www.numdam.org/item/?id=SB_1987-1988__30__165_0
La conjecture ABC, par Gerhard Frey (Univ.
Duisburg-Essen), un article (en français) de Pour la Science :
https://www.pourlascience.fr/sd/mathematiques/la-conjecture-abc-7026.php
La conjecture abc et quelques unes de ses conséquences,
par Émeline Crouseilles et Alexandre Lardeur
sous la dir. de Bernard Le Stum (univ. Rennes 1) :
https://perso.univ-rennes1.fr/bernard.le-stum/bernard.le-stum/Enseignement_files/ABC-CONJECTURE-2.pdf
The ABC Conjecture, par Tom Wright, professeur univ. Caroline du Sud : http://www.math.jhu.edu/~wright/ABC2E.pdf
Beyond the last theorem, par Dorian Goldfeld : http://www.ega-math.narod.ru/Liv/Goldfeld.htm
i Dorian Goldfeld (1947-) : mathématicien américain d'origine allemande, spécialiste en théorie analytique des nombres.
Professeur à l'université Columbia (sise New York). Prix Cole 1987.
Conjecture abc, quelques conséquences, par Michel
Waldschmidt, IMJ-PRG (Institut Math. Jussieu) :
https://webusers.imj-prg.fr/~michel.waldschmidt/articles/pdf/abcFrVI.pdf
Conjecture abc, page d'Eric Weisstein :
https://translate.google.com/translate?hl=fr&sl=en&u=http://mathworld.wolfram.com/abcConjecture.html&prev=search
Nombres riches et conjecture ABC sur le site de Gérard Villemin : http://villemin.gerard.free.fr/aMaths/Factorisation/Riches.htm
Rich numbers, par Ulrich H. Kurzweg (univ.
Floride) :
http://www2.mae.ufl.edu/~uhk/RICH-NUMBERS.pdf
Démonstration de la conjecture de Biberbach par Joseph Oesterlé
(Séminaire Bourbaki, Juin 1985) :
http://archive.numdam.org/article/SB_1984-1985__27__319_0.pdf
Articles de J. Oesterlé sur Numdam : http://archive.numdam.org/search/Oesterlé-"Oesterlé, Joseph"-qn/
» Preuve de la conjecture abc revendiquée par Mohamed Sghiar :
http://www.iosrjournals.org/iosr-jm/papers/Vol14-issue4/Version-1/D1404012226.pdf,
ou bien :
https://hal.archives-ouvertes.fr/hal-01830367/document
» Preuve
contestée de la conjecture abc revendiquée en 2012 par le mathématicien
japonais Shinichi Mochizuki (univ. Kyoto) :
a)
https://www.pourlascience.fr/sr/partenariat-quanta-magazine/les-mathematiciens-se-dechirent-autour...php
b)
https://www.larecherche.fr/mathématiques/la-fin-dune-démonstration-controversée