ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Lord William BROUNCKER, irlandais, 1620-1684

Ce vicomte, mathématicien et physicien, obtint  son doctorat de physique à Oxford en 1647. Brouncker fut aussi chancelier sous Charles II et présida la Royal Society dont il fut cofondateur avec Wren et son ami Wallis.

Certains de ses travaux portant sur la rectification de courbes usuelles (parabole, hyperbole, cubiques) furent publiés par Wallis.

En arithmétique, Brouncker s'intéressa aux équations diophantiennes, dont en particulier l'équation x2 - ny2 = 1 où n n'est pas un carré, équation dite de Pell ou de Pell-Fermat, ainsi qu'aux fractions continues qui leurs sont liées (dont il est le premier à exposer une théorie générale).

»  Diophante , Pell , Fermat
 
Conjecture de Brouncker :

Partant de la formule de Wallis, produit infini calculant π, on doit à Brouncker (1658) une conjecture de développement en fraction continue du célèbre nombre.

Euler et Lambert la prouveront. Ce dernier l'utilisera (entre autres méthodes) afin de prouver l'irrationalité de π.

 ➔   On remarquera le lien subtil entre la formule de Brouncker et celle de Leibniz (également dite de Gregory) :

Si vous calculez les sommes partielles successives de la série ci-dessus, vous trouverez aisément :

1 , 1 - 1/3 = 2/3 , 1 - 1/3 + 1/5 = 13/15 , 1 - 1/3 + 1/5 - 1/7 76/105, ...

Comparez maintenant avec les réduites successives de la 1ère formule de Brouncker... idem :

 

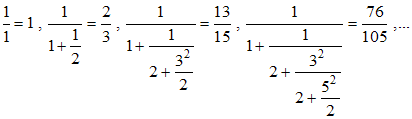
Brouncker procéda sans doute par induction en construisant sa fraction à partir de la série de Leibniz. En effet, la formule de Brouncker peut se justifier en appliquant à cette série une formule d'Euler selon laquelle (» réf.) :

Calcul JavaScript de π selon Brouncker : »

 ➔  Pour en savoir plus sur la formule de Brouncker :

Nicolaus Mercator  Rahn
© Serge Mehl - www.chronomath.com