ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Coniques en tant que courbes algébriques du second degré     » Coniques définies par foyer et directrice  | La parabole | L'ellipse | L'hyperbole

Dans un repère du plan, que l'on peut supposer orthonormé, l'équation générale des courbes algébriques du second degré est de la forme (e) :

ax²  + bxy + cy² + dx + ey + f = 0 , (a,c) ≠ (0,0)           (e)

Afin de prouver que l'équation générale donnée ci-dessus correspond aux coniques (éventuellement dégénérées : point, droites), il nous faut la ramener à une équation plus simple permettant de préciser la nature de la courbe en cherchant principalement à éliminer le terme en xy.

Trois cas fondamentaux se présentent :

1°/  b = 0   

♦  Si ac est nul, par exemple c = 0, on est ramené à y = -ax²/e - dy/e - f/e, équation d'une parabole d'axe parallèle à (Oy).

♦  Si ac est non nul, on regroupe ax² + dx et cy² + ey en écrivant ces trinômes sous la forme canonique :

ax² + cy² + dx + ey + f = a[(x + d/2a)² -d²/4a²] + c[(y + e/2c)² -e²/4c²] + f

(e) peut donc s'écrire :

aX² + cY² = K en posant X = x + d/2a, Y = y + e/2c, K = d²/4a ⁺ e²/4c - f

c'est l'équation réduite d'une conique à centre pouvant s'écrire :

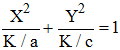
et dont la discussion suivant les signes de K/a et K/c conduisent à une ellipse ou une hyperbole admettant le point Ω(-d/2a,-e/2c) comme centre de symétrie.

Coniques, foyers, directrices, équation réduite des coniques à centre :  »

2°/  b non nul, a = 0 ou bien c = 0   

Traitons le cas c = 0 : l'équation se ramène à une expression rationnelle de y en fonction de x :

On obtient là une hyperbole. Pour s'en convaincre, on effectue la division polynomiale afin de ramener l'équation à la forme :

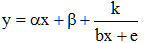
En posant Y = y - αx - β et X = bx + e, c'est à dire en choisissant comme axes de coordonnées les asymptotes de la courbe, on est ramené à l'hyperbole :

XY = k             »  l'hyperbole

Noter que ce changement de repère revient à utiliser la transformation affine :

3°/  b non nul, a ≠ 0, c ≠ 0   

Méthode 1 :   

Procédons comme d'Alembert en posant x' = x, y' = y - αx - β et en calculant α et β afin d'éliminer le terme en xy. Un calcul élémentaire conduit à α = -b/2c (annulation des xy) et β = -e/2c (annulation des y), soit y' = y + (bx + e)/2c. Cela revient à utiliser la transformation affine (simple translation dans le cas b = 0) :

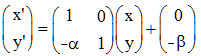
 !    Si le repère était orthonormé, le nouveau repère ne l'est plus !

On reporte dans l'équation (e) qui devient :

(4ac - b²)x'² + 4y'² + (4d - 2be)x' + 4f - b² = 0        (e')

équation que nous pouvons écrire sous la forme :

Ax'² + 4y'² + Bx' + C = 0        (e")

où A = 4ac - b², B = 4d - 2be, C = 4f - b². Voilà une équation bien plus sympathique.

• On reconnaît une parabole si A = 0, soit si 4ac = b².

• Si A est non nul, l'équation peut s'écrire au moyen de la forme canonique du trinôme :

AX² + 4Y² = K    avec cette fois X = x' + B/2A, Y = y' et K = - C + B²/4A

Nous voilà ramenés à l'équation réduite des coniques à centre déjà rencontrée en début d'étude. Plus précisément :

• La courbe admet la nouvelle origine C(-B/2A,-e/2) comme centre de symétrie.

• Le cas A > 0, K > 0 correspond à une courbe fermée limitée par les droites d'équations X² = K/A et Y² = K/4 : ellipse pouvant être un cercle. Noter que les éléments caractéristiques doivent être calculés dans un repère orthonormé (distance euclidienne usuelle).

• Les cas A < 0, K ≠ 0 fournissent une courbe hyperbole.

• Les autres cas correspondent à l'ensemble vide, un point ou des droites.

» Noter que le coefficient A = 4ac - b² apparaît comme un discriminant permettant de distinguer le type de conique étudié.

Méthode 2 :   

Repartons de l'équation initiale en repère orthonormé direct avec a et c non nuls :

ax² + bxy + cy² + dx + ey + f = 0           (e)

L'expression ax² + bxy + cy² est une forme quadratique que l'on peut généralement réduire en une combinaison linéaire de deux carrés par une méthode sophistiquée. Procédons ici de façon élémentaire en tentant d'éliminer le terme en xy au moyen d'une rotation R des axes d'angle θ : si on nomme (x',y') le couple de coordonnées relativement aux nouveaux axes, on a :

          (r)

Ce qui fournit x = x'cosθ - y'sinθ et y = x'sinθ + y'cosθ. On reporte dans (e4) et on obtient l'équation :

 Ax'² + Bx'y' + Cy'² + Dx' + Ey' + f = 0          (e5)

avec :

• A = acos²θ + bsinθcosθ + csin²θ ,  B = (c - a)sin2θ + bcos2θ ,  C = asin²θ - bsinθcosθ + ccos²θ

• D = dcosθ + esinθ , E = -dsinθ + ecosθ.

L'objectif est d'annuler B. Vu que b est non nul, l'équation (c - a)sin2θ + bcos2θ = 0 conduit à cotan2θ = (a - c)/b sous la condition sin2θ ≠ 0, ce qui est assuré car sin2θ = 0 implique bcos2θ = 0, donc cos2θ = 0, ce qui ne se peut.

Sous la condition cotan2θ = (a - c)/b, L'équation (e5) se réduit alors à :

Ax'² + Cy'² + Dx' + Ey' + f = 0

On est ainsi ramené au cas b = 0 traité au début de cette étude pouvant se compléter par la recherche de l'équation réduite et des paramètres de la conique.

Exemple :    

Considérons la courbe d'équation x² + 4xy + y² - 8x - 8y - 9 = 0. On a ici cotan2θ = (a - c)/b, donc 2θ = π/2 [π]. En choisissant θ = π/4, nous sommes conduits à :

3x'² - y'² - 8√2x' - 9 = 0 ,

équation pouvant s'écrire :

3(x' - 4√2/3)² - y'² = 59/3 ou encore 3X² - Y² = 59/3 avec X = x' - x' - 4√2/3, Y = y'

On reconnaît là une hyperbole dont le centre, relativement au nouveau repère, est Ω(4√2/3,0), soit, en revenant au repère d'origine au moyen de la formule (r), expression analytique de la rotation : Ω(4/3,4/3).

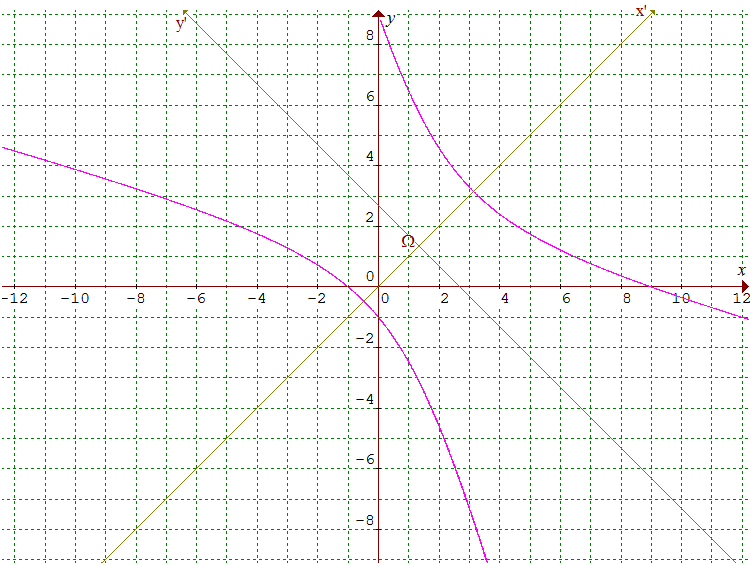
Les coniques, équations réduites, éléments caractéristiques :  »

Méthode 3 :    

Repartons de nouveau avec l'équation initiale en repère orthonormé direct avec a et c non nuls :

ax² + bxy + cy² + dx + ey + f = 0           (e)

Cherchons d'abord à éliminer les termes du 1er degré en x et y par un simple changement d'origine (translation) en posant x' = x - x_o, y' = y - y_o. Un calcul élémentaire conduit à  :

ax'² + bx'y' + cy'²  + (2ax_o + by_o + d)x' + (2cy_o + bx_o + e)y' + f_o = 0           (e''')

avec f_o = ax_o² + bx_oy_o + cy_o² + 2dx_o + 2ey_o + f. L'élimination des termes en x et y est possible si et seulement si on a simultanément :

2ax_o + by_o + d = 0
 bx_o + 2cy_o + e = 0

Le déterminant de ce système est Δ = 4ac - b². On remarque en ce nombre le critère précédemment rencontré.

♦  Si Δ est non nul :    

On obtient une unique solution C pour notre changement d'origine. L'équation se réduit à :

 ax'² + bx'y' + cy'² + f_o = 0          (e4)

La courbe étudiée admet donc C come centre de symétrie : nous l'appellerons le centre de la courbe.

Exemple :    

Considérons de nouveau la courbe d'équation x² + 4xy + y² - 8x - 8y - 9 = 0. Le système s'écrit ici 2x + 4y - 8 = 0, 4x + 2y - 8 = 0 et fournit comme précédemment, et c'est heureux...,  x = y = 4/3 pour le centre Ω.

La rotation autour de Ω conduit aux mêmes calculs :

• A = acos²θ + bsinθcosθ + csin²θ ,  B = (c - a)sin2θ + bcos2θ ,  C = asin²θ - bsinθcosθ + ccos²θ

• D = dcosθ + esinθ , E = -dsinθ + ecosθ.

L'objectif est d'annuler B. Vu que b est non nul, si sin2θ l'est aussi, B = 0 entraînerait cos2θ = 0. Donc sin2θ ≠ 0 et B = 0 équivaut à cotan2θ = (c - a)/b. L'équation (e4) se réduit alors à :

AX² + CY² + f_o = 0

qui est la forme générale de l'équation réduite d'une conique à centre.

♦  Si Δ est nul :    

On se ramène à la méthode 2 en procédant à la rotation autour de l'origine. Il s'agira alors généralement d'une parabole ou de cas triviaux : ensemble vide, points ou droites.

Remarque :     

Seulement cinq des coefficients de l'équation ax² + by² + cxy + dx + ey + f = 0 sont indépendants : il faut donc au plus 5 points pour définir une unique conique passant par ces points. Si un cercle est parfaitement défini par 3 points, la figure de droite montre que 4 points ne peuvent définir une unique ellipse.

Paradoxe de Cramer :  »