ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Tangente à l'ellipse       » Étude générale de l'ellipse | Cercle directeur | Cercle principal | Tangente à l'hyperbole

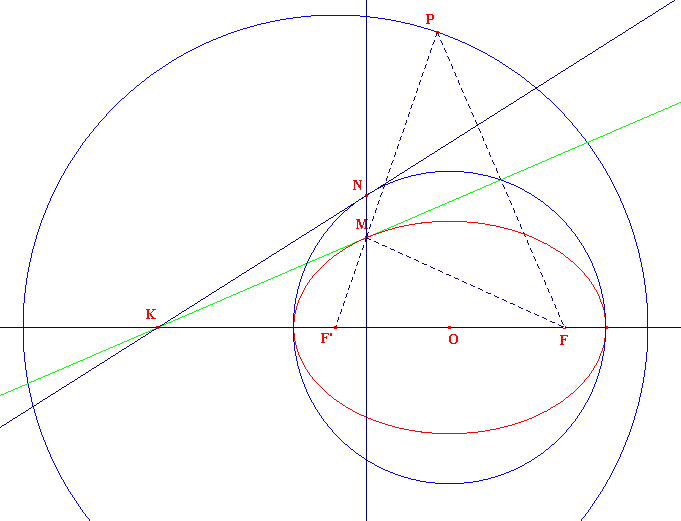
Considérons l'ellipse obtenue comme ensemble des centres M des cercles passant par F tangents intérieurement au cercle de centre F', de rayon F'P = 2a. On a donc MF + MF' = 2a.  » cercle directeur

Soit M' un second point de l'ellipse, centre du cercle tangent intérieurement au cercle directeur en Q. Il s'agit de rechercher si la sécante (M'M) à l'ellipse admet une position limite lorsque M' tend vers M : ce sera la tangente en M.

Le point J, intersection des tangentes au cercle directeur en P et Q, a même puissance par rapport aux deux cercles (m) et (m'). Par conséquent, si nous joignons J à F, la droite (JF) est l'axe radical de ces cercles. Notons H l'intersection de (JF) et (MM') : l'angle ^JHM est droit car l'axe radical de deux cercles est perpendiculaire à la droite des centres.

Faisons tendre M' vers M : Q tend vers P, ainsi que J. La droite (M'M) admet alors comme position limite la perpendiculaire à (FP) passant par M. Par construction de l'ellipse, pour tout M, MF = MP. On peut donc énoncer :

♦  la position limite de (M'M), tangente en M, est la médiatrice de [FP] :

♦  Le symétrique d'un foyer par rapport à la tangente en un point de l'ellipse est situé sur le cercle directeur associé à l'autre foyer

On a ^PMH = ^FMH, ce qui prouve que :

♦ La tangente en M est la bissectrice extérieure de l'angle ^F'FM et la normale en M (perpendiculaire à la tangente) est la bissectrice intérieure de, l'angle ^F'FM (angle des "rayons vecteurs" en M) :

♦  La projection orthogonale d'un foyer sur une tangente à l'ellipse appartient au cercle principal.