
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

» loi exponentielle de paramètre λ |
➔ Cette page demande des connaissances élémentaires relatives aux lois de probabilités dites continues : lois régies par des variables aléatoires pouvant prendre toute valeur d'un intervalle fini ou non de R.
Notion de fonction de répartition (cas discret) : » Variable aléatoire continue, densité : »
En calcul des probabilités, on peut s'intéresser à un phénomène dont une (ou plusieurs) caractéristique(s) ne subit (subissent) pas les injures du temps... Rares sont de tels phénomènes ! Dans la pratique, ils relèvent donc d'événements survenant accidentellement et/ou de façon brutale comme dans la désintégration des atomes radioactifs (cf. in fine). On peut tout au contraire parler de vieillissement en termes de phénomène physique : consulter par exemple cette vidéo de l'Académie des sciences où Alice Guionnet (mathématicienne, ENS/CNRS) parle de ce sujet devant des lycéens à l'occasion de la semaine des mathématiques (mars 2018).
 Durée de vie sans vieillissement
:
Durée de vie sans vieillissement
:
Le disque dur de votre ordinateur à une durée de vie théoriquement très élevée : 100 000 h (on appelle ça le MTBF : Mean Time Between Failures). Si vous l'utilisez, disons 6h par jour, cela vous donne 16666 jours environ d'espérance de vie, soit plus de 45 ans... Dans ces conditions, on peut estimer que s'il ne vous a pas lâché au bout de 8 jours, la probabilité qu'il tombe en panne le 9è jour est la même que la veille : on parle alors de durée de vie sans vieillissement.
 De même, chez un enfant de 5 ans en pleine
santé, on peut estimer que la probabilité de le voir victime d'une crise
cardiaque à 7 ou 8 ans n'a pas évolué. Mais le risque existe ! Chez un homme de
55 ans, considéré jusque là en pleine santé, on est en droit de penser que le
risque a augmenté lorsqu'on s'intéresse à son sort à 60 ans...
De même, chez un enfant de 5 ans en pleine
santé, on peut estimer que la probabilité de le voir victime d'une crise
cardiaque à 7 ou 8 ans n'a pas évolué. Mais le risque existe ! Chez un homme de
55 ans, considéré jusque là en pleine santé, on est en droit de penser que le
risque a augmenté lorsqu'on s'intéresse à son sort à 60 ans...
Ces allégations reposent sur des qualités optimales de fabrication (on n'a pas encore les statistiques sur 100 000 heures de fonctionnement d'un disque dur) ou des statistiques de mortalité relatives, hélas, à certaines maladies.
Étude :
Considérons un phénomène sujet à une durée de vie sans vieillissement, régi dans le temps par une variable aléatoire positive X indiquant sa durée de fonctionnement ou de vie.
En termes de probabilité, en notant [X ≥ α] l'événement "X est au moins égal à α", cette hypothèse signifie, au moyen des probabilités conditionnelles, que :
Pour tout x et tout t positifs : Prob([X ≥ x + t] / [X ≥ t]) = Prob[X ≥ x]
On peut aussi écrire :
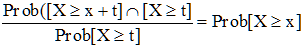
C'est à dire :
Prob([X ≥ x + t] = Prob[X ≥ x]) × Prob[X ≥ t]
Pour tout x ≥ 0, posons φ(x) = Prob[X ≥ x], nous obtenons :
∀ x ≥ 0, ∀ t ≥ 0 : φ(x + t) = φ(x) × φ(t) (1)
La fonction de répartition de X est :
F(x) = Prob[X < x] = 1 - Prob[X ≥ x] = 1 - φ(x)
Recherchons F, dérivable de densité f, c'est à dire vérifiant
F'(x) = f(x) = - φ'(x)
en dérivant la relation (1) par rapport à t, en supposant alors x fixé. nous obtenons :
∀ x ≥ 0 : φ'(x + t) × 1 = φ(x) × φ'(t)
Pour t = 0, on a :
∀ x ≥ 0 : φ'(x) = φ(x) × φ'(0)
➔ φ'(0) est non nul, sinon φ'(x) = 0 pour tout x ≥ 0 entraînerait φ(x) = cte, soit Prob[X ≥ x] = cte. Or [X ≥ 0] est l'événement certain, donc Prob[X ≥ 0] = 1 et, par suite, Prob[X ≥ x] = 1 : notre variable X supposée aléatoire ne l'est plus... : à rejeter !
| Définition de la loi exponentielle de paramètre λ : |
Nous sommes ainsi face à une équation différentielle élémentaire du type φ' = kφ. C désignant une constante arbitraire à déterminer, la solution générale est :
φ : x → C.ekx
D'où l'appellation loi exponentielle, On a φ(0) = Prob[X ≥ 0] = 1, donc C = 1 et :
φ(x) = ekx , F(x) = 1 - ekx , f(x) = F'(x) = -k.ekx
Concernant la constante k, vu que F représente une probabilité, on a nécessairement k < 0. On pose alors λ = - k, paramètre de la loi. En définitive, la fonction de répartition de la loi exponentielle est donnée par :
F(x) = Prob[X < x] = 1 - e-λx, x ≥ 0, λ > 0 (2)
de densité (fonction dérivée de F) :

∗∗∗
Voici un résultat utile, utiliser
(2) ci-dessus :
Vérifier que pour tout couple (a,b) de réels
vérifiant 0 ≤ a < b, on a : Prob(a ≤ X ≤ b) = e-λa
- e-λb
➔ L'espérance mathématique et la variance de cette loi, dont les calculs sont proposés ci-dessous, sont respectivement 1/λ et 1/λ2
∗∗∗



4. Extrait bac 2006,
série S :
La durée de vie d'un appareil avant sa première
panne est modélisée par la loi exponentielle de paramètre 0,2 :
loi de probabilité p exprimée sur R+ par :
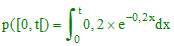
p([0,t[ exprimant la probabilité que l'appareil tombe en
panne avant l'instant t.
Calculer la probabilité que l'appareil tombe en panne au cours des trois
premières années.
Rép :
☼
5. Exercices type baccalauréat Série S (lien externe, sur le site Progresser-en-maths) : »
|
Lien avec la désintégration d'atomes radioactifs : |

La période du radium est le laps de temps nécessaire à la désintégration de la moitié de sa masse. C'est donc, en termes de statistique, la médiane de notre loi exponentielle, à savoir T tel que :
Prob[X > T] = 0,5
Par conséquent, e-λT = 0,5. Ce qui conduit à -λT = ln(0,5), soit T = λ/ln2.
∗∗∗ Radioactivité, période du radium
Les notions d'espérance mathématique et de variance (cas continu) : »
➔ Quelques lois continues étudiées dans ChronoMath :
La loi de Laplace-Gauss, dite normale | La loi de Pearson dite du χ2
- La loi de Student, dite loi t | La loi de Fisher, dite loi F | La loi de Cauchy.
Autres lois étudiées dans ChronoMath : »