ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Quadrilatère complet

Considérons un quadrilatère convexe ABCD qui ne soit ni un trapèze ni un parallélogramme et complétons la figure en prolongeant les côtés [AB] et [CD] d'une part, [AD] et [BC] d'autre part. On obtient les points d'intersection E et F :

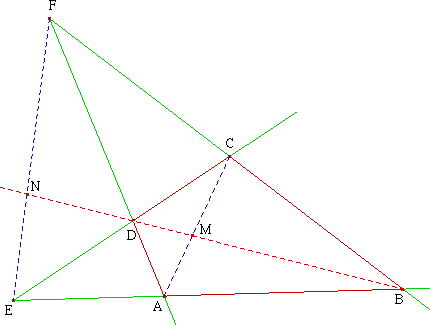
• Les demi-droites [EA), [EC), [FD) et [FB) forment un quadrilatère complet (q) de sommets A, B, C, D, E et F.

• [EA), [EC), [FD) et [FB) constituent les "côtés".

• Les diagonales de (q) sont les droites joignant les sommets opposés, c'est à dire (AC), (BD) et (EF).

Une autre façon de définir un quadrilatère complet est la suivante :

Un quadrilatère complet est la figure constituée par quatre droites coplanaires dont trois quelconques ne sont pas concourantes.

Historiquement, cette figure est étroitement liée à la théorie des transversales de Ménélaüs et de Pappus d'Alexandrie (droites coupant deux côtés d'un triangle) et, plus récemment, à la géométrie projective.

Propriété fondamentale :       

Chaque diagonale est partagée harmoniquement par les deux autres. En particulier, ci-dessous : [B,D,M,N] = -1 ou bien, plus explicitement :

Preuve :

Soit u, le conjugué harmonique de E par rapport à D et C; (Fu) coupe (EB) en v. Le faisceau F(E,u,D,C) est harmonique et il en est donc de même, par intersection de M(E,u,D,C) et M(A,v,A,B).

Or (MA) = (MA) et (MD) = (MB). Les deux faisceaux M(E,u,D,C) et M(A,v,A,B) ayant en commun trois droites sont donc confondus (unicité du conjugué harmonique).

Ainsi (Mu) = (Mv) : M est aligné avec u et v; c'est dire que F, u, M et v sont alignés : la division (B,D,M,N) est harmonique.

Ce résultat permet de construire facilement, à la règle seule :

• le conjugué v d'un point E par rapport à deux point A et B;

• la polaire d'un point E par rapport à deux droites sécantes ou parallèles.

Polaire d'un point par rapport à deux droites : »

 ➔  La figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet : voici un quadrilatère complet ABCDEF. Ses quatre « côtés » sont (ABC), (AFD), (EFB) et (EDC), ses trois diagonales sont (AE), (CF) et (BD) :

 ➔   Pour en savoir plus :

• GEOMETRIE, classe de mathématiques élémentaires par V. Lespinard et R. Pernet, Librairie A. Desvigne - Lyon, 1962.
• Géométrie classique et mathématiques modernes par Brigitte Sénéchal - Formation des enseignants et formation continue - Ed. Hermann - Paris 1979