ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Si l'on sait construire un segment de longueur L, on saura construire la racine carrée de L grâce à une relation métrique dans le triangle rectangle :

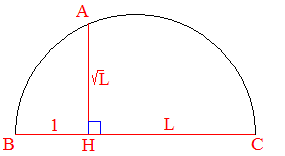
1. Tracer (ci-dessous) un segment [BC] de longueur 1 + L contenant le point H tel que BH = 1.

2. Tracer le cercle de diamètre [BC].

3. Utiliser la relation selon laquelle dans un triangle ABC rectangle en A, si H désigne le pied de la hauteur issue de A, on a l'égalité :

AH² = HB × HC

Pour le cas étudié, on a donc : AH² = L.

4. Élever maintenant depuis le point H la perpendiculaire à [BC]. Elle coupe le demi-cercle en A tel que AH = √L.

 ➔  Et problème est ainsi bien résolu au sens d'Euclide :

» Construction au sens d'Euclide 

» Thalès et la notion de point constructible 

Théodore de Cyrène :  »           Construction de la section dorée :  »