
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
@ Pas de cours, pas de théorie, je veux utiliser le programme JavaScript | Voir le programme Série classée | Paramètres de position : moyenne (espérance mahématique) , médiane , fractiles (quartiles, déciles, centiles) Paramètres de dispersion : écart-type , écart moyen , variance , moments Représentation d'une série statistique : Diagrammes et graphiques | Évaluation graphique de la médiane » Statistique à deux variables (couple aléatoire) |
Rappelons tout d'abord le vocabulaire élémentaire de la statistique (du latin moderne statiticus = qui relève de l'État) :
Enseignée de nos jours dès le collège, la statistique est une branche des mathématiques cherchant à observer et dénombrer des relations qualitatives ou quantitatives sur ce qu'il est convenu d'appeler une population. Ce terme ne désignant pas nécessairement des êtres humains ou des animaux mais des éléments, dits individus, d'un ensemble clairement défini par une ou plusieurs propriétés qui le caractérisent. Les premiers relevés statistiques remontent à Moïse... (» Cardan).
Exemples :
Le résultat des votes (individus) à l'élection
présidentielle française (suffrage universel auprès de la population
majeure) depuis 1958
en fonction de l'étiquette politique
des candidats.
La couleur des yeux (individus : bleus, verts, gris, bruns, noirs, albinos, vairon, ...) indiquée sur les passeports français (population).
Les notes (individus) en mathématiques (arrondies à l'unité) des candidats (population) au baccalauréat français 2015, section TerS.
Le nombre d'accidents mortels (individus) de la
route pendant une période déterminée en fonction des limitations de vitesse
(population)
sur un parcours donné.
|
L'enquête statistique : |
L'objet de cette page est la statistique descriptive consistant à récolter des informations (enquête statistique) sur une population donnée et à évaluer certains paramètres qui lui sont attachés. On parle de sondage lorsqu'on enquête sur une partie de la population et de recensement lorsque toute la population est étudiée.
On devra distinguer entre la statistique descriptive et la statistique inférentielle qui, à partir des données statistiques descriptives permet de formuler des conclusions quant à la population étudiée, quitte à formuler ces conclusions avec une certaine probabilité (marge d'erreur). Eu égard aux données statistiques, le phénomène étudié peut être approché par un modèle mathématique usant de lois de probabilité (on dit aussi distribution de probabilité) établies au cours des siècles, souvent par des astronomes, jugées pertinentes par le statisticien, comme la loi binomiale, la loi de Laplace-Gauss, la loi de Poisson, la loi de Pearson, ...
Index des grandes lois de probabilité sur ChronoMath : »
Les prévisions météorologiques, par exemple, sont de nature inférentielle, résultant d'une étude mathématique complexe (systèmes d'équations aux dérivées partielles) portant sur de nombreuses informations régionales et planétaires : relevés de vitesse du vent, d'hygrométrie (humidité de l'atmosphère), relevés satellitaires, etc. Malgré leurs progrès, ces prévisions sont entachées d'erreurs car malgré des modèles mathématiques assistés par de puissants ordinateurs, une part d'aléatoire subsiste dans les sautes d'humeur de notre planète... Les prévisions à 10 jours, comme celle de AccuWeather sur nos mobiles ne sont pas fiables. Les ingénieurs de la météorologie nationale publient leurs prévisions accompagnées d'un coefficient de fiabilité : échelle de 1 (très peu fiable) à 5 (certain). à 10 jours, on est à 1.
|
Nature d'un relevé statistique, premières notions : |
Ce qui est observé sur les individus d'une population, le phénomène étudié, est également qualifié de caractère. Il peut être quantitatif (nombre) ou qualitatif (propriété, comme la couleur des yeux). Dans le premier cas (quantitatif), on parle aussi de variable qui sera dite discrète (ou discontinue) si elle ne peut prendre que des valeurs isolées et continue lorsque toute valeur est possible dans le champ d'étude considéré. Dans le cas qualitatif, au lieu de "valeurs" possibles du caractère, on parlera de modalités.
➔ Dans le cas de la couleur des yeux donnée en exemple ci-dessus, indiquée sur les passeports, ce caractère n'est pas simple à définir. Le préposé est censé distinguer un il "noisette" d'un il marron, un il gris d'un il gris-vert... (» réf.1). On peut ainsi considérer que la statistique n'est pas une branche exacte des mathématiques. Les résultats dépendent grandement de l'enquêteur et ceux-ci doivent être accompagnés d'une fourchette d'erreur. C'est dire que la statistique s'imbrique dans le calcul des probabilités.
L'ensemble des résultats est une série statistique (numérique ou qualitative). Noter que toute série statistique peut être ramenée à une série de type numérique en associant un nombre à une qualité observée (bleu = 1, vert = 2, ...).
Effectifs et fréquences, mode :
♦ Le nombre d'observations d'une valeur observée (numérique ou qualitative) d'un caractère X est l'effectif de cette valeur. On parle aussi d'effectif partiel afin de bien le distinguer de l'effectif total N de la population : cardinal de l'ensemble des observations : si les valeurs observées du caractère étudié sont x1, x2, ..., xk d'effectifs partiels respectifs n1, n2, ..., nk, on a : n1 + n2 + ... + ek = N.
L'ensemble des couples (xi, ni) i = 1,2,...,k est qualifié de distribution d'effectifs que l'on résume généralement dans un tableau comme on le verra de nombreuses fois par la suite.
♦ Le quotient fi = ni/N de l'effectif d'une valeur ou modalité par celui de la population (effectif total) est la fréquence de cette valeur ou modalité. On l'exprime souvent en pourcentages pour plus de clarté. La connaissance de N et de l'ensemble des fréquences, dite distribution de fréquences, permet celle des effectifs.
On a représenté ci-dessous (nuage de points) 69 notes relatives à 3 devoirs de contrôle consécutifs de mathématiques d'une classe de 4è. Les notes 7 et 13, d'effectif 6 ont pour fréquence 6/69 = 2/23, soit environ 0,087 ou bien, en pourcentages : 8,7%.

➔ On peut bien entendu étudier plusieurs caractères simultanément. Dans le cas de deux caractères X et Y, l'étude corrélative recherchant une relation fonctionnelle f(X,Y) = 0 ou Y = f(X), comme par exemple, dans une école militaire, la taille et le poids de ses soldats, relève d'une étude statistique à deux dimensions.
♦ On appelle mode d'une série statistique numérique, la valeur dont l'effectif est le plus grand ou, ce qui revient au même, la plus grande fréquence. Le mode peut ne pas être unique : on parle de série série bimodale, trimodale, etc. Dans le cas d'un mode unique, la série est qualifiée d'unimodale.
La série de l'exemple ci-dessus comporte deux modes : les notes 7 et 13 ont le même effectif (6). Cette classe apparait hétérogène.
|
Regroupement en classes des données, amplitude, classe modale, effectifs et fréquences cumulées : |
Pour des séries à fort effectif, en particulier concernant des caractères pouvant varier continument (pouvant prendre a priori toute valeur dans un intervalle donné), les valeurs recueillies sont souvent triées et regroupées en un certain nombre de classes.
Dans l'exemple d'un poids, on ne va sans doute pas distinguer deux individus de poids 75 kg et 75,1 kg. Pour des adultes, on peut raisonnablement regrouper les poids par intervalles de 10 Kg : on parle de classes d'étendue ou d'amplitude 10 kg.
D'une façon générale, les classes s'identifient à des intervalles de type [a,b[ (fermé à gauche, ouvert à droite) et on appelle classe modale la classe de plus grand effectif. Comme précédemment, la non unicité peut se produire.
➔ Afin de calculer certains paramètres, il est utile de calculer les effectifs cumulés (ou les fréquences cumulées selon le souhait de l'enquêteur) indiquant pour chaque classe son effectif augmenté de celui des valeurs qui lui sont inférieures.
Le calcul des effectifs cumulés d'une classe s'obtient en ajoutant l'effectif de la classe à l'effectif cumulé précédent (l'effectif cumulé de la 1ère classe étant l'effectif de cette classe). Le dernier effectif cumulé doit égaler l'effectif total de la population (ce qui sert de test pour une éventuelle erreur de calcul). Calcul semblable pour les fréquences cumulées.
Voici un exemple pour une série de 260 poids, regroupés par classes d'amplitude 10 kg.
➔ Remarquer la ligne faisant apparaitre les centres des classes, le centre de l'intervalle [a,b[ étant (a + b)/2. Ces centres seront utilisés dans le calcul de certains paramètres comme la moyenne et l'écart-type : dans une série classée, la valeur prise en compte de la classe est son centre.

Le tableau ci-dessus nous indique que 161 sur 260 personnes ont un poids inférieur à 90 kg.
Il peut être également utile de calculer les effectifs (ou fréquences) cumulé(e)s décroissant(e)s : le calcul des effectifs cumulés décroissants d'une classe s'obtient en soustrayant l'effectif de la classe précédente à l'effectif cumulé précédent (l'effectif cumulé décroissant de la 1ère classe étant l'effectif total de la population). Cette dernière définition implique, en toute logique syntaxique, que la locution effectif cumulé est synonyme d'effectifs cumulés croissants.
|
Représentation des relevés statistiques, diagrammes & graphiques : |
Comme vu ci-dessus, les relevés statistiques sont généralement résumés dans des tableaux pouvant avoir plusieurs entrées (lorsque les caractères observés sont multiples ou liés à un paramètre), par exemple :
La série ci-dessous résume le nombre d'accidents mortels selon les différentes vitesses limite d'un parcours routier de 2000 à 2005 (table de contingence) établissant un lien de dépendance entre vitesse et accident mortel. 136 accidents ont été répertoriés sur 6 années.
|
vitesse lim.
→ |
30 | 50 | 60 | 70 | 90 | 110 | 130 | Total |
| 2000 | 0 | 1 | 1 | 3 | 5 | 6 | 11 | 27 |
| 2001 | 0 | 0 | 2 | 2 | 4 | 7 | 13 | 28 |
| 2002 | 0 | 1 | 1 | 1 | 3 | 5 | 9 | 20 |
|
2003 |
|
|
|
|
|
|
|
|
|
2004 |
0 |
0 |
2 |
1 |
3 |
4 |
9 |
19 |
|
2005 |
0 |
2 |
1 |
2 |
4 |
4 |
8 |
21 |
| Total | 1 | 4 | 7 | 11 | 22 | 31 | 60 |
➔ En statistique, contingence et corrélation sont deux notions distinctes. La contingence entre deux caractères exprime une dépendance sans pour autant pouvoir présumer que l'un serait fonction de l'autre. La corrélation est plus forte et le calcul du coefficient de corrélation peut conduire à établir une relation fonctionnelle entre deux variables statistiques.

♦ Diagrammes :
La légende raconte que Napoléon disait souvent qu'un schéma vaut mieux qu'un long discours. En statistique aussi... Lorsque cela est possible, on utilise des diagrammes : représentation schématique ou graphique des données. On attribue la paternité de ces représentations à l'anglais William Playfair (1759-1823). Introduisons-les sur un exemple simple :
Voici une série de données relative à la circulation sur une route départementale. 1000 véhicules ont été répertoriés. Par "local", on veut signifier que le véhicule est immatriculé dans le département; "périphérique" signifie que le véhicule est immatriculé dans un des départements limitrophes; sinon il est considéré comme "autre" :
 Les
diagrammes ci-dessous :
Les
diagrammes ci-dessous :
synthétisent de façon équivalente le tableau des données.
La hauteur des bâtons et des barres sont proportionnelles aux fréquences (ou aux effectifs suivant le cas voulu). Concernant le diagramme en secteurs, c'est l'angle d'ouverture qui est proportionnelle aux fréquences (ou aux effectifs). La représentation 3D (Microsoft Excel) n'est pas une nécessité ! Le calcul des angles se fait selon les formules :

Pour des raisons relevant du sujet traité, on peut utiliser des formes plus exotiques comme en pyramides ci-dessous...
♦ Graphiques :
Au paragraphe effectifs et mode, on a représenté points par points une série de 69 notes, on parle de nuage de points, représentation rendue possible par un faible effectif total :

➔ Dans le cas d'un tableau statistique où deux paramètres X = (xi) et Y = (yi) sont étudiés corrélativement, la représentation des points Mi(xi,yi) permet de conjecturer un lien fonctionnel de type Y = f(X) entre X et Y :
Régression par méthode des moindres carrés : » ∗∗∗ Sujet BTS info/gestion 1990 » cas d'un couple statistique
Concernant notre série des 69 notes, on peut les regrouper par classes d'amplitude 3 comme ci-dessous :

Ce regroupement conduit au tableau suivant et à un graphique où la série est représentée par des points (x,y), les abscisses portant les centres des classes et les ordonnées, leurs effectifs :
|
notes |
|
|
|
|
|
|
|
|
centres |
1,5 |
4,5 |
7,5 |
10,5 |
13,5 |
16,5 |
19 |
|
effectifs |
2 |
8 |
15 |
12 |
15 |
11 |
6 |
|
effectifs |
2 |
10 |
25 |
37 |
52 |
63 |
|
|
effectifs |
60 |
10 |
25 |
37 |
52 |
63 |
69 |
La liaison des points est facultative; elle renforce l'ensemble des disparités de la distribution des effectifs. Au "second" plan, on a représenté le diagramme en barres des effectifs :
|
Les paramètres de position : moyenne, médiane, fractiles (quartiles, déciles, centiles) : » paramètres de dispersion |
♦ La moyenne :
La notion générale de moyenne d'une série statistique, également appelée espérance mathématique dans le cas de valeurs aléatoires (contexte probabiliste) a été évoquée à la page consacrée à l'astronome et physicien hollandais Christiaan Huygens. Rappelons simplement ici que la moyenne d'une série statistique est la moyenne de ses valeurs pondérées par leurs effectifs.
La notion de moyenne pondérée : »
On doit distinguer deux cas suivant que la série est donnée en extension (on connait toutes les valeurs et, donc, leurs effectifs) ou par regroupement en classes (on connait les centres et les effectifs). Dans ce second cas, on effectue la moyenne des centres pondérés par les effectifs des classes. Voyons cela sur un exemple dans le cas de la série des 69 notes :
Données en extension :

m = (2 × 2
+ 2 × 3
+ 3 × 4
+ 3 × 5
+ 5 × 6
+ 6 × 7
+ ... + 5 × 14
+ ...+ 4 × 18
+ 2 × 19)/69
= 10,724...
≅ 10,7.
Données regroupées :
|
notes |
|
|
|
|
|
|
|
|
centres |
1,5 |
4,5 |
7,5 |
10,5 |
13,5 |
16,5 |
19 |
|
effectifs |
2 |
8 |
15 |
12 |
15 |
11 |
6 |
m = (2 × 1,5 + 8 × 4,5 + 15 × 7,5 + 12 × 10,5 + 15 × 13,5 + 11 × 16,5 + 6 × 19)/69 = 775,5/69 = 11,239... ≅ 11,24.
On voit sur cet exemple une différence, et cela est bien normal, entre les deux calculs (environ un demi-point), à moins d'arrondir à l'unité...
♦ La médiane :
Le concept de médiane d'une série statistique apparaît chez Rujer-Josip Bochkovitch au milieu du 18è siècle. Étant donnée une série statistique triée par valeurs croissantes, elle correspond au nombre, souvent théorique, md tel que 50% des observations lui soit inférieur ou égal et 50% supérieur ou égal. Intuitivement, il y a "autant de chances" d'observer une valeur du caractère inférieure ou supérieure à md (» médiane d'une variable aléatoire).
Si x1 ≤ x2 ≤ ... ≤ xn sont les valeurs observées triées croissantes : il y a autant de xi ≤ md que de xi ≥ md.
Le fait de considérer les inégalités au sens large permet d'assurer l'existence de la médiane dans tous les cas. Sinon, pour une série comme {1 , 2 , 3 , 4 , 5 , 5 , 5 , 6 , 7 }, la médiane n'existerait pas. Au niveau économique et social, ce paramètre est couramment utilisé dans les études statistiques relatives à l'emploi : âge médian, salaire médian.
En 2015, le salaire médian des français s'élevait à 1772 net par mois.
➔ La moyenne et la médiane d'une série restent de piètres paramètres pour tirer la moindre conclusion quant à une série statistique. Elles lissent les inégalités présentes dans les valeurs extrêmes (marginales). Prenons 3 élèves dont les notes sont respectivement 2, 10 et 18. Leur moyenne est 10 : tout juste la moyenne... Les très bonne très mauvaise notes passent inaperçues. La médiane est 10. L'écart-type permet de mieux analyser la situation. Dans les conseils de classes des lycées et collèges, la moyenne règne généralement en maître auprès de la direction et l'écart-type est le grand oublié...
i Rujer-Josip Bochkovitch (1711-1787), ou encore Ruggero-Giuseppe Boscovich, mathématicien et astronome dalmate (Croatie). Il fonda l'Observatoire de Milan où il diffusa les théories newtoniennes (mécanique héliocentrique, théorie de la gravitation). Il sera chargé par le pape Benoît XIV de mesurer l'ellipticité de la Terre. Afin de corriger les erreurs d'observations, cet astronome utilisera une méthode d'ajustement annonçant la célèbre méthode des moindres carrés.
➔ En dehors de cas pédagogiques "fabriqués", la médiane est rarement une valeur observée du caractère étudié mais il ne faut pas s'arracher les cheveux avec la parité de n et l'existence ou non de classes.
Calcul de la médiane en cas de série discrète (n valeurs connues triées par ordre croissant) :
- si n est impair, n = 2p + 1, la médiane est xp+1= x(n+1)/2. Par exemple, pour 7 valeurs observées, distinctes ou non, x4 est la valeur médiane :

Supposons que les 7 valeurs observées du caractère étudié soient 5, 7, 7, 10, 10, 12 ,13, la médiane est 10.
- si n est pair, n = 2p : la médiane est la demi-somme (xp + xp+1)/2. Par exemple, pour 8 valeurs, (x4 + x5)/2 est la valeur médiane :
➔ Si le caractère étudié est évalué en nombres entiers, on pourra s'étonner de donner de possibles résultats décimaux. Ils doivent être interprétés statistiquement. Par exemple, si l'on entend que le nombre moyen d'enfants dans les familles françaises est de 1,5. On doit comprendre, en première analyse que l'on rencontrera le plus souvent des familles de un ou deux enfants.
Supposons que les 8 valeurs observées du caractère étudié soient 5, 7, 7, 10, 10, 12 ,13, la médiane est 4.
Exemple avec 19 notes relevées en vrac {11 , 5 , 8 , 17 , 15 , 9 , 11 , 20 , 3 , 10 , 7 , 10 , 9 , 12 , 15 , 15 , 17 , 7 , 11 } et représentée triée dans le tableau ci-dessous.
xi 3 5 7 8 9 10 11 12 15 17 20 effi 1 1 2 1 2 2 3 1 3 2 1 eff. cumul.
croiss.1 2 4 5 7 9 12 13 16 18 19
La médiane est md = x(19 + 1)/2 = x10 = 11. Cette valeur 11 est répétée 3 fois : x10 , x11 et x12 sont égales à la médiane. Ce n'est pas un problème eu égard à sa définition.
Calcul de la médiane en cas de série organisée par classes, effectifs et/ou fréquences des classes :
Dans le cas des séries classées, on convient d'une répartition uniforme des données dans les classes. Le calcul des fréquences cumulées permet de déterminer la médiane proportionnellement à la fréquence de la classe qui la contient sans se poser la question de savoir si l'effectif total est pair ou non. Voyons cela sur un exemple :
La série ci-dessous résume les résultats (164 notes) obtenus en mathématiques dans un centre d'examen. Les notes de 0 à 20, arrondies au demi-point, sont groupées par classes de même amplitude. Pour plus de clarté, les fréquences affichées, exprimées en pourcentages, sont arrondies au dixième tout en restant cohérentes afin que leur somme égale 100%. En fait, dans les calculs, nous nous servirons ultérieurement des fréquences exactes (quotient eff. / eff._total). On reviendra sur ce point après le calcul de la médiane.
|
classes |
|
|
|
|
|
|
|
|
|
|
|
centres |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
|
effectifs |
5 |
12 |
15 |
30 |
28 |
40 |
16 |
11 |
3 |
4 |
|
effectifs |
5 |
17 |
32 |
62 |
90 |
130 |
146 |
157 |
160 |
164 |
|
fréquence |
3,1% |
7,5% |
9,3% |
18,6% |
17% |
24,4% |
9,8% |
6,7% |
1,8% |
2,4% |
|
fréquences |
3,1% |
10,6% |
19,9% |
38,5% |
54,9% |
79,3% |
89% |
96% |
97,6% |
100% |
Au vu des fréquences cumulées, nous constatons que la médiane md (50%) appartient à la classe [8,10] (classe médiane) d'amplitude 2, de fréquence 17% (28/164). On sort de la classe précédente à 38,5%. Jusqu'à 50%, nous avons 11,5%. L'accroissement de la note de 8 à md représente alors 11,5 dix-septièmes des 2 points d'amplitude. La médiane est donc :

Les notes étant arrondies au demi-point, nous concluons que la médiane peut être évaluée à 9,5 : il y a globalement autant de candidats (82) qui ont moins ou plus de 9,5/20 à cet examen.
➔ D'une façon générale, on peut écrire la formule du calcul de la médiane md. Pour cela, notons : c1, c2, ... les classes, ci celle de la médiane qui contient 50% des données cumulées, vi la valeur d'entrée dans la classe ci (borne inférieure de cette classe), ai l'amplitude de la classe médiane. Les fréquences étant écrites en pourcentages, on a :

Remarques :
Dans cet exemple, nous avons utilisé les valeurs approchées des fréquences. Lorsque l'effectif total est élevé, cela ne modifie pas ou peu la valeur de la médiane. Mais on peut éviter toute discussion en utilisant les effectifs. La formule précédente s'écrit alors :

Appliquons cette formule à notre exemple, plus simple d'emploi et évitant les risques d'accumulation d'erreurs d'arrondi :

valeur que nous pouvons encore arrondir à 9,5.
Évaluation graphique de la médiane par interpolation linéaire :
Montrons qu'une médiane peut être évaluée graphiquement en traçant le graphique des effectifs (ou fréquences) cumulés croissants ou décroissants, voire les deux à la fois. Reprenons ce cas déjà étudié :
|
poids en kg |
|
|
|
|
|
|
|
centres |
65 |
75 |
85 |
95 |
105 |
115 |
|
effectifs |
7 |
36 |
118 |
70 |
23 |
6 |
|
effectifs |
7 |
43 |
161 |
231 |
254 |
260 |
|
effectifs |
260 |
253 |
217 |
99 |
29 |
6 |
Comme dit dans le paragraphe précédent, on suppose uniforme la distribution des données dans chaque classe. C'est dire que la représentation graphique d'une borne d'une à l'autre est linéaire (segment de droite). La borne supérieure d'une classe correspondant à la borne inférieure de la suivante, la représentation graphique des effectifs cumulés croissants est continue. C'est donc celle d'une fonction F continue, affine par morceaux (en bleu ci-dessous) :

On a F(60) = 0 puisque les éléments de la 1ère classe [60,70] son censés se répartir uniformément dans cette classe. L'effectif total de la population est 260. F étant strictement croissante de [60,120] sur [0,260], il existe une unique valeur md de l'intervalle [60,120] telle que F(md) = 260/2 = 130. On trace la droite d'équation y = 130. Elle correspond (sensiblement) sur l'axe des abscisses à 8. La médiane de cette série peut donc être évaluée à 87 kg. Costauds les gars...
➔ On pourra vérifier ce résultat "à la main" ou bien utiliser le programme JavaScript présent sur cette page. On pouvait tout aussi bien utiliser la représentation graphique des effectifs cumulés décroissants. La juxtaposition des deux graphiques dans le même repère montre une intersection correspondant à la médiane.
On notera que le graphique admet y = md comme axe de symétrie :

➔ Au lieu des effectifs cumulés, la représentation des fréquences cumulées est tout aussi valable sachant que l'on tracer dans ce cas la droite d'équation y = 1/2.
∗∗∗
Variante pour le calcul d'une médiane par interpolation linéaire
♦ Les quartiles :
On peut encore affiner la répartition des valeurs d'une série statistique au moyen des premier et troisième quartile :
Le premier, noté Q1, est théoriquement égal à la valeur du caractère tel que 25% (un quart) des observations lui soit inférieur (75% sont supérieures).
Le troisième, noté Q3 correspondant au nombre tel que 25% lui soit supérieur (75% sont inférieures).
Le second quartile, que l'on pourrait noter Q2, n'est autre que la médiane M définie ci-dessus.

La connaissance des quartiles permet de marginaliser les extrêmes de la série en estimant plus significatif l'intervalle interquartile [Q1,Q3]. Ce faisant, on rejette 50% de la population statistique : c'est beaucoup. C'est pourquoi, lorsque les effectifs le permettent, on a recours aux déciles et centiles évoqués au paragraphe suivant.
Dans le cas, par exemple de 77 observations, 25% de 77, à savoir 19¼, n'est pas un nombre entier. Q1 pourra être le 19è élément (25%, arrondi de19,25) ou le 20è ou encore la moyenne pondérée (x19 + 3x20)/4 et Q3 sera le 58è (arrondi de 57,75).
Dans le cas de la série des 19 notes, l'application théorique des 25% (rang 4,75 arrondi à 5) et 75% (rang 14,25 arrondi à 14) conduit à Q1 = 8 et Q3 = 15 :
xi 3 5 7 8 9 10 11 12 15 17 20 effi 1 1 2 1 2 2 3 1 3 2 1 eff. cumul.
croiss.1 2 4 5 7 9 12 13 16 18 19
19 étant impair, la médiane M est en x10 = 11.
x1 • • • x5=Q1 • • • • x10=M • • • x14=Q3 • • •x19
Mais par souci de symétrie, il est plus logique de pondérer en estimant les quartiles comme des médianes de demi-séries :

Remarques pour un choix plus subtil des quartiles : »
♦ Les déciles et les centiles :
Les statisticiens ont alors défini les déciles (au nombre de 9) partageant la série en 10 sous-effectifs correspondants à 10%, 20%, ... 90% de l'effectif total de la population étudiée, et aussi les centiles (au nombre de 99) correspondant à 1%, 2%, ...99%. Par exemple, le 3ème décile est théoriquement égal à la valeur du caractère tel que 30% des observations lui soit inférieur (70% sont supérieures).
➔ Pour de petits effectifs, les notions de quartiles n'ont guère d'intérêt, encore moins les déciles et les centiles : l'étude d'une série d'observations mérite une étude statistique permettant d'établir des informations dignes d'intérêt sur la population étudiée dès lors que son effectif est au moins de l'ordre de la centaine, voire plusieurs milliers.
Dans le cas de séries classées, ces paramètres de position (quartiles, déciles centiles) se calculent de la même façon que la médiane en remplaçant 50% des effectifs par 25%, 75%, 10%, 1%, etc.
|
Les paramètres de dispersion : variance, écart moyen arithmétique, écart-type : |
Les notions de variance et d'écart-type d'une série statistique ont été évoquées dans le cadre statistique et du calcul des probabilités à la page consacrée à l'astronome et physicien hollandais Christiaan Huygens. Le lecteur pourra s'y reporter. Nous les détaillons ici en introduisant un troisième paramètre tombé en désuétude :
Soit (xi) = (x1, x2, ..., xn) une série statistique de n relevés (quantitatifs). On peut en calculer la moyenne m et s'intéresser à la dispersion (déviation) des valeurs xi autour de cette moyenne. Pour cela, il on pourrait calculer les écarts xi - m et en faire la moyenne. Mais des écarts au-dessus et au-dessous de la moyenne pourraient se compenser. En fait, ils se compensent globalement !
Preuve : la somme des écarts est Σ(xi - m) = (x1 - m) + (x2 - m) + ... + (xn - m) = Σxi - nm = Σxi - n(Σxi /n) = 0.
On peut alors utiliser :
♦ L'écart moyen arithmétique :
Soit (xi) = (x1, x2, ..., xn) une série statistique de n valeurs distinctes de moyenne m dont on note effi l'effectif de la valeur xi relevée. On appelle écart moyen arithmétique la moyenne des valeurs absolues des écarts | xi - m |, écarts arithmétiques, pondérés par leur effectif :

Si on note frqi la fréquence de la valeur xi, on peut aussi écrire, avec l'opérateur de sommation Σ :

Ce nombre, relativement délaissé, peut être intéressant pour des études statistiques peu poussées où moyenne et dispersion autour de cette moyenne s'avèrent suffisantes pour tirer des conclusions.
Exemple : reprenons le cas des 19 notes. La moyenne est m = (3 + 5 + 14 + ... + 34 + 20)/19 = 212/19 ≅ 11,16, que nous arrondissons à 11.
xi 3 5 7 8 9 10 11 12 15 17 20 Total effi 1 1 2 1 2 2 3 1 3 2 1 19 effi x xi 3 5 14 8 18 20 33 12 45 34 20 212 |xi - m| 8 6 4 3 2 1 0 1 4 6 9 /// effi x |xi - m| 8 6 8 3 4 2 0 1 12 12 9 65 L'écart moyen arithmétique est em_a = (8 + 6 + 8 + ... + 12 + 9)/19 = 65/19 ≅ 3,42, que nous arrondissons à 3,5 : en moyenne, les écarts sont de 3,5 points autour de la moyenne. Évaluée à 11, cette moyenne laisse penser que le groupe a un niveau acceptable. Mais on peut considérer que l'éventail significatif des notes est l'intervalle [m - em_a, m + em_a] = [7,5;14,5]. Les autres notes sont marginales (élèves faibles ou brillants...). Le groupe semble donc plutôt hétérogène. Voir la même série avec le calcul de l'écart-type dont la définition est donnée ci-après.
♦ L'écart-type ou écart quadratique moyen :
Pour des raisons pratiques d'ordre mathématique, relatives au calcul des paramètres d'une variable aléatoire continue (à densité, en termes de probabilités) renvoyer, lesquels font appel au calcul intégral, les spécialistes préférèrent remplacer les écarts arithmétiques par leur carré | xi - m |2 = (xi - m)2, calculer leurs somme pondérée (moyenne quadratique) et en prendre la racine carrée. Introduit par Huygens, avec la variance (ci-après), ce nombre, dit écart quadratique moyen, est aussi appelé écart-type et généralement noté σ :
 (frqi désigne effi/n, fréquence de
xi)
(frqi désigne effi/n, fréquence de
xi)
Dans le cas précédent, avec la moyenne arrondie à 11 :
| xi | 3 | 5 | 7 | 8 | 9 | 10 | 11 | 12 | 15 | 17 | 20 | Total |
| effi | 1 | 1 | 2 | 1 | 2 | 2 | 3 | 1 | 3 | 2 | 1 | 19 |
| |xi - m| | 8 | 6 | 4 | 3 | 2 | 1 | 0 | 1 | 4 | 6 | 9 | /// |
| (xi - m)2 | 64 | 36 | 16 | 9 | 4 | 1 | 0 | 1 | 16 | 36 | 81 | /// |
| effi x (xi - m)2 | 64 | 36 | 32 | 9 | 8 | 2 | 0 | 1 | 48 | 72 | 81 | 353 |
On a σ2 = (64 + 36 + ... + 72 + 81)/19, soit : σ = √(353/19) ≅ 4,31. On voit que ce résultat diffère de l'écart moyen de 1 point. C'est beaucoup pour une statistique portant sur des données de faibles valeurs. Mais une estimation reste une estimation. Et bien que l'usage de l'écart moyen semble ici plus naturel, il n'y a pas lieu, dans le cas général, de choisir l'un plutôt que l'autre.
♦ La variance :
La variance V évalue la moyenne pondérée des carrés des écarts par rapport à la moyenne m des données. On parle parfois de fluctuation pour désigner ce nombre :
 (frqi désigne effi/n, fréquence de xi)
(frqi désigne effi/n, fréquence de xi)
Elle doit sa définition dans la mesure où elle apparait fréquemment dans les calculs relatifs à l'étude statistique des séries de données (covariance, corrélation). En développant le carré (xi - m)2, on établira facilement l'intéressante formule, dite de König ou de Huygens :

Autrement dit :
la variance n'est autre que la moyenne des carrés des xi diminuée du carré de la moyenne des xi, que l'on peut encore résumer en la moyenne des carrés moins le carré de la moyenne.
Cette formule permet un calcul plus aisé de la variance et de l'écart-type :
| xi | 3 | 5 | 7 | 8 | 9 | 10 | 11 | 12 | 15 | 17 | 20 | Total |
| effi | 1 | 1 | 2 | 1 | 2 | 2 | 3 | 1 | 3 | 2 | 1 | 19 |
| xi2 | 9 | 25 | 49 | 64 | 81 | 100 | 121 | 144 | 225 | 289 | 400 | /// |
| effi xi2 | 9 | 25 | 98 | 64 | 162 | 200 | 363 | 144 | 675 | 578 | 400 | 2718 |
Avec m = 11, on a σ2 = 2718/19 - 112 ≅ 22,053, soit σ ≅ 4,7 : on est à 4 dixièmes du σ calculé précédemment. On est là encore victime d'erreurs d'arrondi... En conservant la valeur exacte m = 212/19, on obtient σ2 =18,5540..., soit σ = 4,307 comme précédemment.
Moralité :
Toujours utiliser (si possible) les valeurs exactes lors de calculs intermédiaires
➔ Le lecteur physicien ne manquera pas de rapprocher le calcul de la variance et celui d'un moment d'inertie (» Huygens). Les statisticiens définissent également d'autres paramètres de dispersion appelés moments d'ordre k :
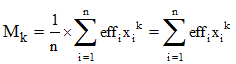
et les moments centrés d'ordre k, la variance étant le moment centré d'ordre 2 :

∗∗∗
Étude d'un tableau statistique
Une série statistique étant donnée en vrac (triée ou non) ou en classes d'amplitudes distinctes ou non, le programme ci-dessous calcule l'effectif total, la moyenne, l'écart moyen arithmétique, l'écart-type, la médiane et les quartiles et, à la demande, les déciles et centiles.
➔ Pour en savoir plus :