
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|
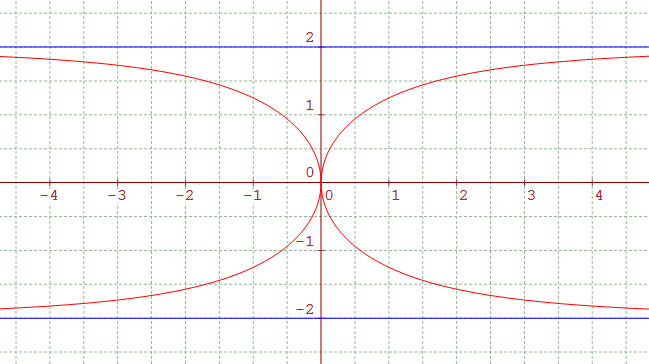
Cette courbe algébrique du 4ème degré (quartique) fut étudiée dès le 17è siècle par Isaac Barrow dans ses Lectiones Geometricae (1674) ainsi que par Isaac Newton, son élève, et Jean Bernoulli dans le cadre du calcul différentiel.
En voici une définition géométrique "modernisée" :
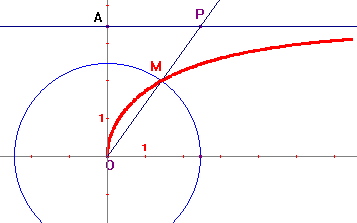
Dans un repère orthonormé d'origine O, soit A(0,a) un point d'ordonnée positive. Soit P un point mobile situé sur la parallèle à Ox passant par A; le cercle de centre O, de rayon AP, coupe [OP) en M. Lorsque P varie, M décrit un kappa (que l'on complète par symétrie par rapport aux axes de coordonnées).
L'équation polaire de cette courbe s'obtient très facilement : en posant (Ox,OM) = t, on obtient immédiatement r = a.tan(π/2 - t), soit :
r = a/tan t
➔ De cette équation, on déduit une équation paramétrique de la courbe Kappa :
x = a.(1/sin t - sin t) , y =a.cos t
! L'équation cartésienne peut être obtenue en élevant au carré les expressions de x et y (ce n'est pas une transformation régulière, les signes de x et de y sont perdus) : on obtient une courbe de centre O admettant (Ox) et (Oy) comme axes de symétrie et les droites d'équations y = ± a comme asymptotes horizontales :
x2(a2 - y2) = y4
que l'on établira aisément à partir de l'équation paramétrique.
! Choisir y = ± a dans l'équation cartésienne x2(a2 - y2) = y4, conduit à 0 = y : prudence, nous somme ici en présence d'une équation implicite d'une courbe algébrique ! Le fait d'obtenir cette valeur contradictoire signifie une indéfinition ou une valeur asymptotique :
Courbes algébriques : »
➔ On reprend ci-dessous les trois Kappa selon Barrow, Newton et J. Bernoulli, étudiées géométriquement au moyen du logiciel Cabri-Géomètre dans sa version CabriJava pour l'Internet et animées par CheerpJ :
|
|


Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération du Kappa selon Barrow
: déplacer P; pour effacer le lieu
double-cliquer dans la figure
|
|
Selon H. Brocard et T. Lemoyne (» réf. 1), l'illustre Isaac Newton, élève de Barrow, reprit l'étude de ce dernier dans son traité sur la Méthode des fluxions sous la forme suivante :
Dans un repère orthonormé, un angle droit ^OMP se déplace de sorte que P glisse sur [Ox), MP garde une mesure constante et [MP) passe par O; dans ces conditions M décrit un kappa (on complète la courbe par symétrie par rapport aux axes de coordonnées).


Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération du Kappa
selon Newton
: déplacer P; pour effacer le lieu
double-cliquer dans la figure
|
|
Jean Bernoulli définit ainsi le kappa :
Dans un repère orthonormé, on place A(0,a), a > 0, et on considère le cercle de
diamètre [OA]; Soit B un point du demi-cercle supérieur. La médiatrice de [OB]
coupe le cercle en J (d'ordonnée positive). La
parallèle à (Ox) passant par J coupe [OB) en M.
Lorsque B décrit le demi-cercle
supérieur, le point M décrit un
kappa
(on complète la courbe par symétrie par rapport aux axes de coordonnées).


Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération du Kappa
selon
Jean Bernoulli
: déplacer B; pour effacer le lieu
double-cliquer dans la figure
➔ Pour en savoir plus :