ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Spirale hyperbolique               Asymptote en coordonnées polaires , Autres spirales dans ChronoMath

Courbe étudiée par le physicien français Pierre Varignon en 1704. L'équation, en coordonnées polaires de cette belle spirale est, tout simplement :

 L'équation r = a/t explique le nom de la courbe vu que y = 1/x est l'équation de l'hyperbole équilatère en coordonnées cartésiennes. Elle est tracée ci-dessus pour a = 1 et t > 0. Lorsque t varie sur R^* tout entier, on obtient une branche complémentaire symétrique par rapport à Oy puisque le changement de t en - t change le signe de r :

Un zoom en se restreignant à t >0 : r = 1/t , t > 0

 La spirale hyperbolique est plus compliquée qu'elle ne paraît car elle possède non seulement :

• un point asymptote, à savoir l'origine puisque si t tend vers l'infini, r tend vers 0;

• mais aussi une droite asymptote d'équation y = 1 dont elle s'approche infiniment près (par définition d'une telle droite) lorsque t tend vers 0.

On peut prouver ce dernier résultat en utilisant une méthode spécifique aux coordonnées polaires ou bien très facilement en passant aux coordonnées paramétriques (x = r.cos t, y = r.sin t). On a ici, puisque
r = 1/t :

Si t tend vers 0 par valeurs positives, cos(t) tend vers 1, donc x tend vers +, et y = sin(t)/t tend vers 1.

Ce dernier résultat est facile à prouver en remarquant que sin(t)/t = (sin t - sin 0)/(t - 0). Le quotient sin(t)/t apparaît donc comme le taux d'accroissement de sin t au voisinage de zéro et par suite sa limite en 0 est le nombre dérivé de sinus en 0, soit cos 0 = 1.

 Un cas beaucoup plus élémentaire d'asymptote droite, bien connu dès la classe de Première, est donné par l'hyperbole.

Voir aussi  Asymptote oblique :

Notons que la spirale hyperbolique apparaît comme la projection conique (projection centrale) d'une hélice circulaire lorsque le centre de la projection est choisi sur l'axe de cette dernière :

Dans un repère orthonormé (0,x,y,z), l'équation de l'hélice d'axe Oz le long d'un cylindre de rayon R, est de la forme :

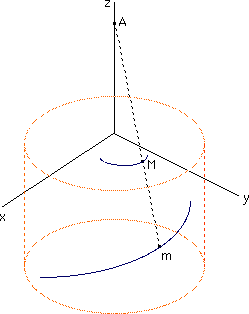
Choisissons A(0,0,a) comme centre de la projection conique. Notons m(x,y,z) un point de l'hélice et M le point projeté sur le plan xOy. Pour chaque t, la droite (Am) est dirigée par (Rcos t , Rsin t, at - a) et pour tout point M(X,Y,Z) de (Am), on peut alors s'écrire :

Le point projeté M(X,Y,Z) est défini par Z = 0 donc par l(1 - t) = 1. D'où :

         (coordonnées paramétriques)

Donc, en coordonnées polaires :

On retrouve bien la spirale hyperbolique, quitte à poser t' = 1 - t.

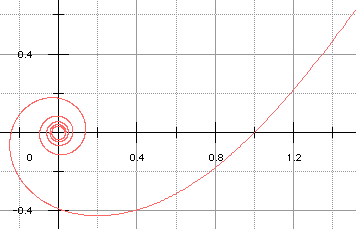
 Si nous projetons sur le plan xOy la partie de l'hélice pour laquelle z est négatif, t = 1 correspond au plan de projection qui doit être écarté (on obtient la branche infinie lorsque t tend vers 1. Ci-dessous, la courbe est tracée pour a = 1 et t variant de -10p à 1.

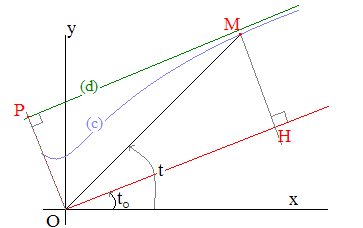
Soir r = f(t) l'équation polaire d'une courbe (c). La recherche d'une telle droite (d) ne se fera que si r tend vers l'infini (branche infinie) au voisinage d'une valeur finie t_o de t. Notons H la projection orthogonale du point M de (c) sur la droite d'angle polaire t_o. L'asymptote (d) existera si et seulement si MH admet une limite finie lorsque t tend vers t_o, c'est à dire si et seulement si le nombre :

existe et est fini. Ce nombre k représentera la distance algébrique OP = HM de l'asymptote au pôle (l'origine des coordonnées), cette asymptote étant parallèle à la droite d'angle polaire t_o. Une valeur positive (resp. négative) de k correspond à un angle orienté (OH,OP) = +p/2 (resp. -p/2). Dans certains cas l'étude du signe de k - r x sin(t - t_o) sera nécessaire pour étudier la position de la courbe par rapport à l'asymptote.

Si k existe mais est infini, il s'agira d'une branche parabolique dans la direction de l'axe polaire t_o.

Si k n'existe pas : r x sin(t - t_o) n'admet pas de limite en , il s'agira d'une branche infinie dans la direction de l'axe polaire t_o. Comme dans le cas cartésien, on peut parler de direction asymptotique d'angle polaire t_o.

Astuce !

Le produit r x sin(t - to) se présente sous la forme indéterminée x 0. Posons alors r = 1/r; le produit conduit à la forme 0/0 et en lui appliquant la règle du marquis de L'hospital, la limite est cos(t - to)/r' où désigne la dérivée de r au point t. Par suite k = 1/r' tout simplement !

1.   Dans le cas ci-dessus de la courbe définie par r = 1/t au voisinage de t = 0, on a immédiatement k = 1. La droite polaire d'angle 0 est l'axe des abscisses. Le nombre k est positif : l'équation de l'asymptote oblique est y = +1.

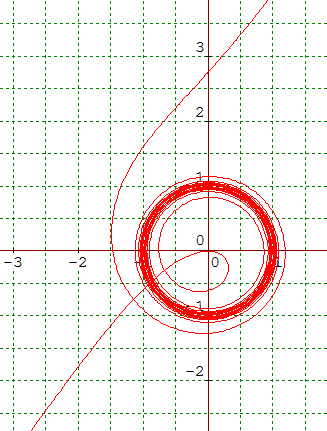
2.   Considérer maintenant la courbe définie par :
Justifier que cette courbe admet un cercle asymptote pour t infini mais qu'au voisinage de t = 1, il ne s'agit que de branches infinies

3.   Étude de la strophoïde (BTS bureau d'études 1971)