ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 BAIRE René
Louis,
français, 1874-1932 |
| BAIRE René
Louis,
français, 1874-1932 |
Normalien, agrégé de mathématiques (1895), tout d'abord professeur de lycée à Troyes, Baire se rend en Italie à l'instigation de Jules Tannery, son professeur à l'ENS, et suit les cours de Volterra et Dini. Il soutiendra sa thèse à Milan en 1899 portant sur l'étude de la Continuité des fonctions limites de fonctions continues.
Baire fut professeur à l'université de Montpellier (1902-1905) puis à Dijon. De santé fragile dès l'enfance, malade et dépressif il dut se retirer en 1914. Il reçut le prix Francoeur (1920) pour l'ensemble de ses travaux. Baire passa les dernières années de sa vie à Lausanne (Suisse). Il se suicidà à Chambéry le 5 juillet 1932.
Ce grand mathématicien français est l'auteur d'importants travaux en topologie générale, sur la notion de dimension topologique, sur une nouvelle théorie des fonctions numériques (classification en différents types) et sur le concept de semi-continuité (apparue dans sa thèse) qui permettra, en particulier, et avec la théorie de la mesure de Borel, la mise en place d'une nouvelle théorie de l'intégration édifiée par Lebesgue.
» Hausdorff Notion de topologie : »
| Parties rares, parties maigres, espace de Baire : |
Dans un espace topologique E, une partie A de E est dite rare si le complémentaire de son adhérence est dense dans E (partout dense). Une partie maigre est une réunion finie ou dénombrable de parties rares.
On qualifie d'espace de Baire un espace topologique E dans lequel toute intersection dénombrable d'ouverts denses dans E est un ouvert dense dans E. Certains mathématiciens considèrent E séparé.
1a/ Un espace topologique E est un espace de Baire si et seulement si le complémentaire de toute partie maigre de E est dense dans E.
1b/ Un espace topologique E est un espace de Baire si et seulement si tout ouvert non vide de E est non maigre.
2/ Tout espace topologique localement compact est un espace de Baire.
3/ Tout espace métrique complet est un espace de Baire.
! L'énoncé réciproque de 2/ est faux : il existe des espaces de Baire non complets : considérer tout simplement R privé de Q !
Espace polonais : »
| Théorème de Baire-Banach : |
Toute application linéaire continue et bijective d'un
espace de Banach
vers un espace de Baire est bicontinue
(c'est à dire continue ainsi
que sa réciproque).
| Fonction de Baire, tribu de Baire : |
E désignant un espace topologique, on nomme ainsi toute limite simple d'une suite de fonctions continues de E dans R.
» Ce sont les fonctions de classe 1. La classe 0 est celle des fonctions continues. De façon récurrente, les fonctions de classe n sont les limites simples des fonctions de la classe n-1.
| Fonctions semi-continues : |
Soit E un espace topologique et xo un point de E. Une fonction f de E dans R est dite :
semi-continue inférieurement (en abrégé sci) en xo si :
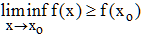
ce qui peut s'écrire :
∀ε > 0, ∃V, voisinage de xo, tel que : ∀x ∈V, f(xo) < f(x) + ε
semi-continue supérieurement (en abrégé scs) en xo si :
ce qui peut s'écrire :
∀ε > 0, ∃V, voisinage de xo, tel que : ∀x ∈V, f(x) < f(xo) + ε
➔ La semi-continuité sur une partie A de E exprime la semi-continuité en tout point de A. On remarquera qu'une fonction continue en un point est une fonction semi-continue inférieurement et supérieurement en ce point. Noter aussi que f est sci (resp. scs) si et seulement si - f est scs (resp. sci).
! La semi-continuité inférieure (resp. supérieure) est à distinguer de la continuité à gauche (resp. à droite).
Considérons par exemple f(x) = E(-x), partie entière de l'opposé de x, représenté en rose sur le graphique ci-dessous. f est continue à gauche en tout n de Z et semi-continue supérieurement en un tel point (dans le voisinage V considéré, on a f(x) = n ou f(x) = n - 1) :
Selon la remarque précédente, g(x) = -f(x) = -E(-x) est encore semi-continue inférieurement et continue à gauche.
∗∗∗
Montrer que la fonction x
→ E(x) et x
→ -E(x)
sont continues à droite, la première étant scs, la seconde sci.
Théorème du point fixe de Kakutani : »
➔ Pour en savoir plus :
Dickson