ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

WREN Christopher, anglais, 1632-1723

Astronome à Oxford, illustre architecte du royaume à Londres : on lui doit en particulier le mausolée de la reine Marie (Westminster), le palais royal de Winchester et (à droite) la construction de la cathédrale Saint-Paul dont la construction s'étala sur 35 ans de 1675 à 1710.

Contemporain en Angleterre de Neile, de Wallis et de Newton, on lui doit des travaux sur le calcul différentiel et intégral naissant. Professeur d'astronomie à Oxford, il fut l'un des premiers élus (1663) à l'Académie Royale de Londres (la Royal Society).

Dans ces années 1660, il se distingue par des projets architecturaux et le terrible incendie de la ville de Londres sera pour lui l'occasion, avec la participation du physicien et géomètre Robert Hooke, de montrer ses talents.

Wren fut le premier (1658) à calculer la longueur d'une arche de cycloïde (baptisée alors roulette par Pascal de 9 ans son aîné). Il ne fit pas appel au calcul intégral dont les outils, à l'époque, n'étaient n'étaient pas suffisamment développés, mais à une astucieuse méthode géométrique propre à la nature de la roulette : admettant intuitivement et expérimentalement qu'une demi-arche mesure m = 4r (r désignant le cercle roulant) et en inscrivant la courbe entre deux familles de polygones, à la manière d'Archimède pour la mesure du cercle, il raisonne par l'absurde en supposant m > 4r puis m < 4R et aboutit dans les deux cas à une contradiction (» réf. 1).

De nos jours, on peut ainsi procéder ainsi : si l'équation de la cycloïde est écrite sous la forme paramétrée :

x = r.(t + sin t) ,  y = r.(1 + cos t) , t décrivant R

en différentiant, on a :

dx/dt = r.(1 + cos t) ,  dy/dt = -r.sin t 

et, d'après les notations et les résultats concernant la rectification d'une courbe :

ds = (dx2 + dy2)½ = 2r.cos(t/2)dt

Par raison de symétrie, La longueur L d'une arche peut être ainsi calculée :

 »  Leibniz , Fagnano , Barrow
 

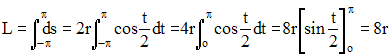
 ➔   Pour en savoir plus :

Barrow  Le Clerc
© Serge Mehl - www.chronomath.com