
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 Otto Hölder naquit à Stuttgart et
fit ses études supérieures
à l'université de Berlin où il eut
Weierstrass
comme professeur. Mais c'est à Tübingen qu'il soutiendra une thèse sur la
théorie du potentiel sous la houlette de
Du Bois-Reymond (1882).
Otto Hölder naquit à Stuttgart et
fit ses études supérieures
à l'université de Berlin où il eut
Weierstrass
comme professeur. Mais c'est à Tübingen qu'il soutiendra une thèse sur la
théorie du potentiel sous la houlette de
Du Bois-Reymond (1882).
Après avoir enseigné à Göttingen et Königsberg, Hölder obtiendra une chaire à Leipzig (1899), poste qu'il conservera jusqu'à sa retraite.
On lui doit d'importants résultats en analyse fonctionnelle mais il se tournera vers la logique, les structures algébriques (théorie des groupes finis) et l'axiomatisation des mathématiques dans le cadre des fondements des mathématiques où il perçoit les limites de la théorie des ensembles et les contradictions qui peuvent naître d'un formalisme outrancier.
| Inégalité de Hölder pour les séries et les intégrales : |
Dans le cas de l'intégrale d'un produit, si f et g sont positives et intégrables sur [a,b], et si p et q sont supérieurs à 1 avec 1/p + 1/q = 1, alors leur produit est intégrable et :
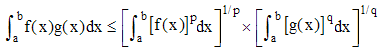
Si p = q = 2, cette relation n'est autre que celle de Cauchy-Schwarz. Cette inégalité est plus généralement valable pour des fonctions de Lp, ensemble des (classes de) fonctions mesurables de puissance p-ème intégrable :
Si f et g sont respectivement éléments de Lp et Lq , alors f × g est élément de L1 (f × g est intégrable) et :
|| f × g ||1 ≤ || f ||p × || g ||q
Espaces Lp : » Inégalité de Minkowski : » Espaces de Hilbert : »