ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Calcul d'une intégrale curviligne        niveau Sup

On se propose de calculer l'intégrale généralisée ci-dessous, dite de Dirichlet, au moyen du théorème des résidus :

La fonction f : x→sin(x)/x, prolongée en 0 par f(0) = 1, est étudiée sur cette page. Grâce à ce prolongement, elle est continue et dérivable sur R. En voici une représentation graphique pour x ≥ 0 :

La courbe est du type oscillatoire amorti : lorsque x tend vers l'infini, f(x) tend vers 0 en oscillant autour de l'axe des abscisses. On remarque que la première demi-arche a pour hauteur 1, sa base mesurant π/2 (valeur qui annule le sinus). La courbe étant concave sur [0,π/2], l'aire de cette demi arche est strictement supérieure à π/2.

On remarque également que chaque arche "sous" l'axe des abscisses est partiellement compensée par celle qui lui succède. On en déduit que si l'intégrale cherchée est convergente, elle peut être inférieure à π/2. Nous allons montrer que J est en fait égale à π/2.

On passe dans le champ complexe en considérant la fonction g : x→e^iz/z que nous allons intégrer sur un contour évitant la singularité en z = 0 :

On considère la demi-couronne circulaire (Γ) ci-contre, réunion de [AB], l'arc (a1), [CD] et l'arc (a2). Le rayon OA mesure R > 0, le rayon OB mesure r > 0. Sur ce contour ne contenant pas 0, la fonction g est holomorphe et selon le théorème de Cauchy, son intégrale est nulle :

En posant z = x + iy, on a :

Considérons les deux intégrales sur [AB] et[CD] en changeant x en -x dans la première :

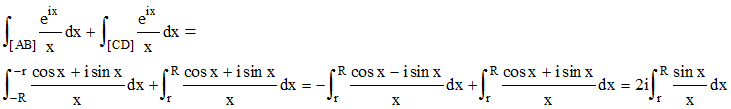
Donc :

Lorsque r tend vers 0 et R vers + ∞ :

• Le membre de droite tend vers 2i × J.

• Dans le membre de gauche :
  - la fonction z →e^iz/z est holomorphe sauf en z = 0 qui est un pôle simple. L'intégrale le long de (a1) est calculée sur un demi-cercle (donc un arc d'ouverture π) parcouru dans le sens négatif. En vertu des théorème 2 et 3 de la page relative au théorème des résidus, cette intégrale vaut donc r_-1 × iπ où r_-1 désigne le résidu de z →e^iz/z au point z = 0. Or e^iz = 1 + iz - z²/2! -iz³/3! + ... Le développement de Laurent de z →e^iz/z est donc e^iz/z = 1/z + i - z/2 - iz²/6 + ... : r_-1= 1 (coefficient de z^-1 = 1/z).
   
  - L'intégrale le long de (a2) tend vers 0 en vertu du théorème 3.2 de la page relative à l'intégrale d'une fonction complexe.

Finalement 2i × J = iπ, soit :