ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Résolution d'un système différentiel linéaire 3x3       » système différentiel 2x2

On considère le système différentiel linéaire du 1er ordre, de dimension 3 :

1. On pose pour simplifier : x' = dx/dt , y' = dy/dt et z' = dz/dt. Montrer que l'on peut écrire :

2. Montrer que les valeurs propres de la matrice :

 

sont 0, 2 et - 2 et que M est diagonalisable au moyen de la matrice de la matrice de passage :

3. Déduire des résultats précédents que, relativement à la base de vecteurs propres calculée ci-avant, le système peut s'écrire :

X' = 0 , Y' = 2Y , Z' = -2Z  avec

et que, finalement :

La méthode se généralise à une dimension quelconque et se conduit semblablement lorsque la matrice est "seulement" triangulable. Dans ce cas, on obtient une matrice de la forme :

On obtient d'abord Z, puis Y et X par résolution de deux équations linéaires du 1er ordre.

Prenons le cas de l'exercice résolu à la page triangulation : on obtenait la matrice triangulaire

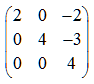
On a alors :

• Z' = 4Z, donc Z = k.e^4t, k∈R.
• Y' = 4Y - 3Z, soit Y' - 4Y = k.e^4t : équation linéaire du 1er ordre; on obtient facilement :
  Y = (kt + m)e^4t, m∈R.
• X' = 2X - 2Z, soit X' - 2X = -2k.e^4t, conduisant à X = p.e^2t - k.e^4t, p∈R

Certains systèmes peuvent conduire à des valeurs propres complexes. Les solutions sont alors généralement complexes. Voici un exemple (cousu de fil blanc...) où la solution complexe contient des solutions réelles :

Les valeurs propres sont ici 0 et ±i. On travaille donc dans C et la matrice de passage permettant la diagonalisation peut être choisie égale à :

On trouve facilement :

a, b et c sont ici complexes, mais si on choisit a réel et b = c = k/2, k réel, on obtient une famille de solutions réelles (» formules d'Euler) :