ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude des matrices de Markov d'ordre 2       niveau Sup        valeurs propres, diagonalisation

On appelle matrice de Markov d'ordre 2, toute matrice carrée de M₂(R) à termes positifs telle que la somme des termes de chacune de ses lignes soit égale à 1. Dans toute la suite, par matrice de Markov, on sous-entend une telle matrice d'ordre 2.

1°) Montrer que toute matrice de Markov d'ordre 2 est de la forme :

où a et b désignent des nombres réels positifs ou nuls n'excédant pas 1.

2°) Montrer que le produit de deux matrices de Markov est une matrice de Markov.

3°) A quelle condition sur a et b une matrice de Markov d'ordre 2 est-elle inversible ? L'inverse d'une matrice de Markov est-elle une matrice de Markov (discuter) ?

4°) On considère la matrice de Markov M définie par a = 1/4, b = 3/4, c'est à dire :

a - Calculer les valeurs propres de M.

b - Montrer que tout matrice de Markov admet λ = 1 comme valeur propre. Exprimer la seconde valeur propre en fonction de a et b.

5°) R² est considéré comme espace vectoriel sur R muni de sa base canonique (i, j),  i = (1,0), j = (0,1). On considère l'endomorphisme de R² admettant M comme matrice (définie en 4°).

a - Calculer les vecteurs propres u et v de M associés aux valeurs propres calculées en 4° b, u étant associé à la valeur propre 1.

b - Vérifier que (u,v) est une base de R² et exprimer la matrice D de f dans cette base. En déduire Dⁿ pour tout entier naturel n.

c - Exprimer Mⁿ dans la base (i, j).

1°) et 2°) : bien évident !

3°) Une matrice est inversible si et seulement si son déterminant est non nul. Dans le cas d'une matrice de Markov M, on a det(M) = a - b. La condition est donc a ≠ b. Sous cette condition, on a :

                      »  matrice inverse

La somme des lignes est bien égale à 1 mais les termes doivent être positifs.

• Si  a - b  > 0, les termes 1 - b et a sont positifs car a et b n'excèdent pas 1, mais il nous faut aussi - b et a - 1 positifs, ce qui n'est possible que si b est nul ainsi que a - 1 : b = 0, a = 1 : on obtient la matrice unité :

• Si  a - b  < 0, les termes 1 - b et a doivent ici être négatifs , ce qui n'est possible que si 1 - b est nul ainsi que a : b = 1, a = 0 : on obtient la matrice :

Et dans ces deux cas triviaux, on constate que M = M^-1.

4°) a - On calcule P(λ) = det(M - λI), I désignant la matrice unité. Soit :

Les valeurs propres sont donc 1 et -1/2.

b - D'une façon générale P(λ) = det(M - λI) = λ² - λ(a - b + 1) + (a - b). On remarque en effet que P(1) = 0. La seconde solution est alors a - b.

5°) a - Mu = u conduit à u(1,1) et Mv = - ½v conduit à v(1,-1); det(u,v) = -2, donc (u,v) est une base (orthogonale) de R².

b - On exprime f(u) et f(v) dans la base (u,v)  : f(u) = u(1,0), f(v) = -½v(0,-½). Donc :

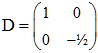
C'est une matrice diagonale comme on pouvait s'y attendre.

 ➔  Mais pourquoi faire simple quand on peut faire compliqué :

La matrice de passage P est :

Son inverse est :

La matrice de f dans la base (u,v) est alors P^-1MP, soit :

_________________________

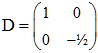
On a alors :

c - Il nous faut calculer f ⁿ(i) et f ⁿ(j) dans la base (i,j).

• f ⁿ(u) = u =  i + j.
  Par conséquent f ⁿ(i + j) = f ⁿ(i ) + f ⁿ(j) =  i + j.

• D'autre part f ⁿ(v) = (-½)ⁿv = (-½)ⁿ (i - j).
  Par conséquent f ⁿ(i - j) = f ⁿ(i ) - f ⁿ(j) =  (-½)ⁿi - (-½)ⁿj.

De ces calculs, on déduira aisément f ⁿ(i ) et f ⁿ(j) pour obtenir :

1.  Au moyen de la matrice de passage P, on aurait obtenu le même résultat (cette fois plus rapidement...) au moyen de la formule M = PDP^-1, donc Mⁿ = PDⁿP^-1.

2. On voit que Mn admet une limite pour n infini : » état stationnaire, ergodicité.