
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
➔ Cette simple et efficace correction est présentée ici comme un intéressant exemple du puissant usage du tableur dans une démarche d'observations, de conjectures et d'essais, base de la démarche scientifique. Elle est due à un collègue belge, Claude Pierroux, qui la calcula à des fins pratiques en 1974, alors qu'il enseignait les sciences à l'Institut Provincial d'Enseignement Technique de Seraing (Belgique) et que les calculatrices de l'époque n'étaient pas encore programmables et ne possédaient pas les fonctions de l'analyse combinatoire.
On sait que la factorielle de n est le nombre :
La formule de Stirling donne une approximation de ce produit :
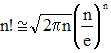
Notons ε(n) l'erreur absolue commise au moyen de cette approximation :

Comme l'indique le tableau ci-dessous, où les nombres sont exprimés en notation scientifique à deux décimales, l'erreur absolue grandit très vite avec n, mais ce qui nous intéresse est bien évidemment ici l'erreur relative ε(n)/n! qui reste faible :
Cependant, on peut vouloir affiner l'approximation de Stirling afin de diminuer sensiblement l'erreur absolue pour de "faibles" valeurs de n. Les considérations expérimentales ci-dessous permettent d'exhiber un bon facteur ε(n)/S de correction et d'apporter une amélioration substantielle dans le calcul approché de n! pour les faibles valeurs de n selon la formule :


En colonnes E et F, l'erreur relative r(n) = ε(n)/S décroît avec n. Si cette décroissance est de type exponentiel, la représentation graphique de la fonction ln r(n) doit être sensiblement linéaire en vertu de la l'équivalence :
y = k.eax ⇔ ln y = ax + ln k
ln désignant le logarithme népérien
Mais il n'en est rien comme le prouve le graphique ci-dessous effectué par le tableur à qui il fut inséré la colonne des logarithmes népériens de ε(n) /S :

Un ajustement exponentiel étant rejeté, il peut s'agir d'une décroissance hyperbolique, c'est à dire du type r(n) = k/(an + b). Pour s'en assurer, demandons au tableur de nous représenter les variations de l'inverse h(n) de notre erreur relative en fonction de n (colonne G du tableau). Si la courbe obtenue est linéaire, c'est gagné car, sous l'hypothèse hyperbolique, l'inverse de r(n) est de la forme a'x + b' avec a' = a/k et b' = b/k.
On a confirmation de la vraisemblance de cette hypothèse :

On peut donc estimer que les inverses h(n) des erreurs relatives commises sont en progression arithmétique. La colonne G indique que q = 12 est une valeur ... raisonnable de la raison de cette progression. Basons nous sur n = 10 afin d'évaluer notre correction :
Finalement :
Les valeurs fournies ainsi par cette formule améliorée sont présentes en colonne P;
La colonne L présente l'arrondi à l'entier le plus proche de la colonne P : elle fournit la valeur exacte de n! jusqu'à n = 10;
La colonne K indique l'erreur relative.

Cette formule, que nous baptisons formule de Stirling-Pierroux en l'honneur de notre collègue, est d'autant plus remarquable qu'elle coïncide avec le développement asymptotique à l'ordre 2 de la fonction Γ d'Euler :
On sait que si x est entier, alors Γ(x) = (x - 1)! et par conséquent :
xΓ(x) = x!
Lorsque n est grand, on a sensiblement :
on peut écrire :
soit :
Par suite, en remplaçant dans la formule de Stirling-Pierroux , on a pour un entier x = n grand :

ce qui correspond bien à x.Γ(x) = x! eu égard au début du développement de la fonction Γ qui s'écrit :

Pas mal !...