ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Trapèze & bissectrices , trapèze & diagonales , trapèze isocèle |
On considère un trapèze ABCD de bases (côtés parallèles) [AB] et [CD];
On note J et K les milieux respectifs de [AD] et [BC].
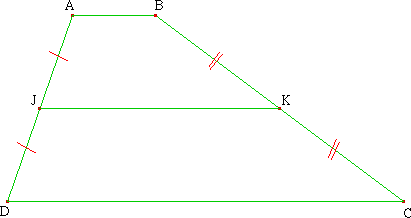
Montrer que JK est la moyenne arithmétique de AB et CD. Autrement dit :
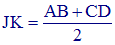

| Solution : |

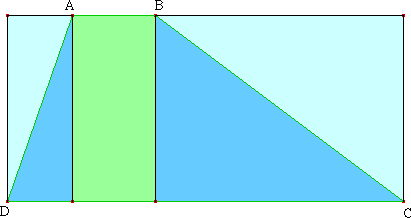
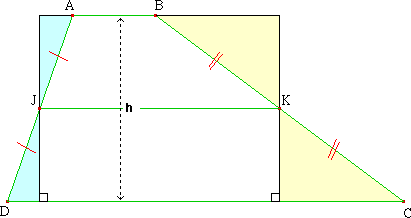
La figure ci-dessous
montre qu'un
certain rectangle, dont la largeur est la hauteur h du
trapèze, a même aire que ce dernier.
D'accord ?
Et tu n'ignores pas que l'aire d'un trapèze est donnée par la formule célèbre :
![]()
Par conséquent, le produit JK × h mesure l'aire du trapèze ABCD; c'est bien dire que :
JK = (AB + DC)/2
» Ce résultat montre que si h reste constant, les trapèzes obtenus en faisant pivoter [AD] ou [BC] autour de leurs milieux respectifs ont même aire.
Si tu as oublié la formule donnant l'aire du trapèze de bases b et B, de hauteur h, il te faut contempler la figure ci-dessous :