ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Coronavirus, ajustement exponentiel par la méthode des moindres carrés     TP niveau Ter/Sup | Ajustement logistique

Rappel :   

La propagation d'un virus, lorsqu'elle n'est pas contrôlée par des mesures sanitaires, est généralement régie par une loi exponentielle du type t → e^αt (e est la base des logarithmes népériens, α paramètre réel). On constate en effet que pour un court laps de temps Δt, le nombre de malades observé y est proportionnel au temps (facteur α) et à la valeur de y à l'instant t considéré :

En termes différentiels, pour un Δt infinitésimal, la relation s'écrit dy/dt = α × y, On montre alors, en classe terminale, que y est une fonction exponentielle du type t → y_oe^α(t-to) où y_o désigne la valeur de y au temps t_o et e la base des logarithmes népériens (» voir par exemple cet exercice). On peut aussi écrire y = k.e^αt en posant k = y_oe^-αto.

Suite géométrique et fonction exponentielle : »              Équations différentielles linéaires du 1er ordre : »          

 ➔  Si l'on préfère un ajustement exponentiel de type f(x) = kα^x, il suffit de poser α = e^a.

Nous appliquons ce résultat théorique à l'évolution du nombres de malades atteints
par le Covid-19 entre les 1er et 18 mars 2020.


représentation graphique obtenue grâce au logiciel Graphmatica

♦ 2. Posons :

f(t) = 118.932 × e^0.257t

^{Dans le repère précédent, la courbe d'interpolation (ci-dessous en beige) s'ajuste parfaitement jusqu'au 15 mars. Quelques jours auparavant, le directeur général de la Santé nous apprenait que le nombre de cas recensés doublait tous les 3 jours. Vérifions cette assertion :}

• f(t + 3)/f(t) = 118.932 × e^{0.257(t + 3)} / 118.932 × e^0.257t = e^0.257×3 = e^0.771 ≃ 2,162.

Le DGS a donc raison. Le nuage s'infléchit à partir du 15 mars pouvant laisser penser que l'on pourrait tendre vers un plateau, maximum de la vague épidémique. Il est trop tôt, avec 4 données, pour une telle conclusion.

Source : https://www.ledevoir.com (La Presse canadienne, 12/03/20)

♦ 3. Puisque le nuage de points s'avère coïncider sur les 15 premiers jours avec une fonction exponentielle t → f(t) = k.e^at, on se propose ici de la rechercher au moyen des contraintes f(t + 3) = 2f(t) pour tout t ≥ 0 et f(15) = 5421. Montrer que cela conduit à :

a = ln(2)/3 ≃ 0,231  et  k = 5421/2⁵ ≃ 169,406, soit :

f(t) = 169,406 × e^0.231t (représentée ci-dessous en bleu)

La courbe s'ajuste fort bien sur le nuage de points, renforçant l'hypothèse du directeur général de la Santé.
Il faut espérer maintenant que cette belle courbe exponentielle va s'effondrer au plus vite, à condition que les irresponsables, pour ne pas dire les abrutis, se promenant encore béatement sur les quais de Seine et de Saône, finissent par comprendre ce qu'est un confinement dans l'intérêt de tous et en particulier de leur famille, de leurs enfants et d'eux-mêmes.
A suivre...
page mise en ligne le 19 mars 2020

page rédigée le 7 avril 2020

En 1798, dans son Essai sur le principe de population, l'économiste anglais Thomas Malthus (1766-1834) affirmait à l'époque un accroissement exponentiel des populations (progression géométrique) et prédisaitt, en admettant une croissance linéaire des ressources alimentaires (progression arithmétique), une paupérisation globale du royaume. Prônant la limitation des naissances, il estimait en outre, que venir en aide aux plus démunis est susceptible de les encourager à procréer en accentuant ainsi le problème de la démographie...

C'est dans un mémoire intitulé Recherches mathématiques sur la loi d'accroissement de la population, paru en 1844, que le mathématicien belge Pierre Verhulst (1804-1849), un ancien élève de Quételet et de Dandelin, introduit l'ajustement logistique dans le but d'étudier un modèle moins pessimiste du devenir d'une population. Verhulst estimait que sans passer par des mesures drastiques, une bonne gestion des ressources et une bonne répartition de la population en fonction de ces dernières (une bonne logistique au sens d'organisation) devaient pouvoir modérer l'accroissement exponentiel et conduire à un équilibre.

Mathématiquement, cela signifie que la courbe représentant l'effectif de la population en fonction du temps admet une limite supérieure (c'est ce que l'on appelle en ces temps d'épidémie le plateau). Le temps n'étant pas limité, il s'agit d'une asymptote horizontale. La fonction d'ajustement proposé par Verhulst est de la forme (» psp) :

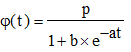 ,  t ≥ 0 , a et p strictement positifs, b ≥ 1.

Et maintenant, un peu de maths. Dans notre cas d'étude, la population est représentée par les personnes dont l'infection par le virus est confirmée.

♦ 4. On étudie ici la fonction φ sur R tout entier. Le plan est rapporté à un repère orthogonal. Montrer que :

a) φ est strictement croissante.

b) lim _t→∞ φ(t) = p.     c) lim _t→-∞ φ(t) = 0.

c) la courbe admet un point d'inflexion Ω d'abscisse 1/a × ln(b), d'ordonnée p/2.

♦ 5. On pose y = φ(t) et y' = φ'(t), fonction dérivée de φ, et k = a/p.

a) Montrer que y vérifie l'équation différentielle y' = k × y(p - y).

 ➔   L'égalité ci-dessus peut s'écrire dy = k × y × (p - y) × dt. Ce qui signifie que l'accroissement dy de la population pendant un court laps de temps dt est proportionnel à l'instant dt, à l'effectif de la population à l'instant t et, ce qui est ici un des objectifs de cette étude, au complément de y relativement à p. Ainsi, lorsque t augmente, p - y tend décroît vers 0; ce coefficient apparait comme un modérateur de la croissance de la population. A partir du point d'inflexion Ω, la courbe s'infléchit : la dérivée diminue et tend vers 0 t(au voisinage de l'asymptote horizontale y = p) tout en restant positive.

On se place maintenant dans le repère d'origine Ω. On pose X = t - 1/a × ln(b) et Y = y - p/2.

b) Vérifier que l'on a Y' = k × (p²/4 - Y²), Y' désignant la fonction dérivée de Y par rapport à t.

c) Soit f une fonction numérique dérivable sur R, nulle en 0, de fonction dérivée f'. Donner une primitive de x → f'(-x).
    Établir l'équivalence : f paire (resp. impaire) ⇔ f' impaire (resp. paire).
       
d) En déduire que la courbe représentative de φ admet Ω comme centre de symétrie.

e) Retrouver ce résultat par le calcul de Y en fonction de X.

Si vous séchez après avoir bien cherché : ››››

♦ 6. Représentations graphiques du nuage de points au moyen de l'outil d'interpolation de Graphmatica : l'abscisse 0 correspond au 29 février 2020.

On constate que l'ajustement exponentiel (en rouge foncé), d'équation y = 245 × 1,19^x n'est désormais plus adéquate (calculée à partir des données du 29/02 au 07/04).

• L'ajustement logistique (en vert), y = 103865,2308 / (1+ 272,4209 × e^-0,1794x), avec les données du 29 février (abscisse 0, 100 cas confirmés) au 3 avril (abscisse 34, 64438 cas confirmés) est remarquable par son adéquation.
  La courbe tend à "s'écraser" légèrement, ce qui est très bon signe :

• Depuis le 3 avril, les données s'ajustent sur la courbe logistique bleue y = 98072,1144 / (1+ 282,7904 × e^-0,1843x); on pourrait commencer à parler de pic à l'abscisse 50, soit le 20 avril et à espérer accéder au plateau dont l'ordonnée serait de l'ordre de 98 000 cas (asymptote horizontale).

Il faudra encore attendre plusieurs jours avant de pouvoir affirmer que l'épidémie recule, mais on voit que le confinement a réussi à infléchir la courbe des cas confirmés de corona virus : en l'absence d'alternative, c'est là, la seule bonne logistique au sens de Verhulst, on serait sans doute sinon sur la courbe exponentielle avec 216520 cas confirmés et une mortalité dramatique !

Mise à jour du vendredi 10/04

Pas réjouissant :    

• le 8 avril, on lâche la courbe bleue;

• le 9 avril, on rattrape la courbe verte (+4342 cas);

• le 10 avril, la situation persiste avec 90676 cas confirmés (+4286). Une nouvelle interpolation logistique produit la courbe rose
  d'équation y = 104893,2894 / (1+ 251,3506e^-0,1756x) indiquant p ≈ 105 000.

- Fin d'étude -

Les statistiques de la source Santé publique France prennent désormais en compte, depuis une dizaine de jours, un nombre croissant de tests PCR (prélèvement dans le nez et la bouche, Polymerase Chain Reaction) et sérologiques (par prise de sang), ce qui fausse l'évolution du nombre de cas confirmés, objet de cette étude : toute conclusion quant au décrochage du nuage par rapport à la courbe logistique du 3 avril (en bleu) est donc sans fondement.

Nous n'avons pas étudié ici le nombre de décès dus au Covid-19.
Là encore, les autorités de santé mettent la pagaille dans leurs statistiques puisqu'on a appris le 7 avril dernier que l'on comptait désormais les décès au sein des EHPAD et autres établissements de soins pour personnes âgées, ce qui aurait dû évidemment être comptabilisé dès début mars.

Les deux diagramme ci-dessous sont cependant encourageants (source Wikipédia, 11 avril 2020), le nombre d'hospitalisations (second diagramme) laisse espérer le plateau tant attendu :

Espérons que le déconfinement dont on parle tant et trop, ne sera pas décidé à la hâte par démagogie, manque d'autorité ou visées politiques. Sans véritables masques de protection, sans mesures barrières efficaces dans les commerces et transports publics, il risque de replonger le pays dans un état de désolation meurtrier.

Quoi qu'il en sera, prenez bien soin de vous !

 ➔  Pour en savoir plus :

1. Pierre-François Verhulst et la loi logistique de la population :
   https://journals.openedition.org/msh/pdf/2893

2. Modélisation et analyse mathématiques de systèmes dynamiques en épidémiologie (pages 16 et suivantes) :
   https://tel.archives-ouvertes.fr/tel-00633827/document

3. a) La notion de système dynamique (ChronoMath) : ..\anx\syst_dyn.html
   b) Systèmes dynamiques et applications en sciences de la vie (univ. Lyon 1) :
   Biologie mathématique et modélisation (pages 23 et suivantes) :
   http://spiralconnect.univ-lyon1.fr/spiral-files/download?mode=inline&data=3324086

4. Statistiques de la maladie du Covid-19 :
   a) France sur Wikipedia (très complet) : https://fr.wikipedia.org/wiki/Pandémie_de_Covid-19_en_France
   b) France & Monde : https://www.eficiens.com/coronavirus-statistiques/#evolution-contamination-france
   c) Information Corona virus (gouvernement) : https://www.gouvernement.fr/info-coronavirus

3. f(t + 3) = 2f(t) ⇔ k.e^{a(t + 3)} = 2k.e^2at  ⇔  k.e^at × e^3a = 2k.e^at  ⇔  e^3a = 2 ⇔ 3a = ln(2). On a donc a = ln(2)/3.
   Si t = 15, at = 5ln(2); d'où f(15) = 5421 = k × e^5ln(2) = k × e^ln(2)×5 = k × [e^ln(2)]^×5 = k × 2⁵. On a donc bien k = 5421/2⁵.

Étude de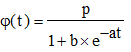

4. a) φ'(t) = abp × e^-at/(1 + be^-at)² > 0 pour tout t. φ croît donc strictement.

b) facile...

c) φ''(t) = bpa²e^-at ×(1 - be^-at)/(1 + be^-at)³ est du signe de  1 - be^-at  s'annulant en t tel que e^-at = 1/b, soit -at = -ln(b); ce qui fournit t = 1/a × ln(b). En cette abscisse φ(t) = p/(1 + b × 1/b) = p/2. Finalement : Ω d'abscisse 1/a × ln(b), d'ordonnée p/2.

5. a) On peut écrire y' = φ'(t) = ap × (be^-at + 1 - 1)/(1 + be^-at)² = ap/(1 + be^-at) - a/p × p²/(1 + be^-at)² = ay × [1 - 1/p × y].
     Donc y' =  a/p × y × [p - y] = k × y × (p - y)  avec k = a/p.

b) On vérifie facilement que Y' = k × (p²/4 - Y²), Y' est donc une fonction paire.

c) Une primitive de x → f'(x) est, par définition, x → f(x) et une primitive de x → f'(-x) = - (-1) × f'(-x) est x → -f(-x).

 i  D'une façon générale, la fonction dérivée de x → f(f o u)(x) = f(u(x)) est x → u'(x) × f'(u(x)); une primitive d'une fonction dérivée composée f'(u(x)), comme ci-dessus f'(-x), peut donc être obtenue à condition d'avoir ou de faire apparaître en facteur la dérivée de u (» dérivation des fonctions composées).

• Si f est paire alors f(x) = f(-x) pour tout x; en dérivant, on constate f'(-x) = -f'(-x) : la fonction dérivée est impaire.

• Inversement si f' est impaire, alors f'(-x) = -f'(x) pour tout x. On sait que deux fonctions ayant même dérivée différent d'une constante (» primitive) . Donc -f(x) = -f(-x) + C, soit f(-x) = f(x) + C. Mais f(0) = 0, donc C = 0 et f est donc paire.

• On raisonnerait de même dans le cas f impaire.

» parité, axe & centre de symétrie 

d) Y est une fonction de X dont la dérivée est paire. Or Y est nulle en X = 0 puisse que la courbe passe par la nouvelle origine Ω. D'après c), Y est une fonction impaire de X. C'est dire que la courbe représentative de φ admet Ω comme centre de symétrie.

e) On reporte t = X + 1/a × ln(b) et y Y = y + p/2 dans y = φ(t) = p/(1 + be^-at), ce qui conduit à Y = p/(1 + e^-aX) - p/2. On met p/2 en facteur et on obtient finalement Y = p/2 × (1 - e^-aX)(1 + e^-aX). Le changement de X en -X change Y en p/2 × (1 - e^aX)(1 + e^aX) qui n'est autre que son opposé : on s'en convaincra en multipliant haut et bas par e^-aX dans cette expression : Y est donc bien une fonction impaire de X.