ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Exposant selon l'Encyclopédie de Diderot et d'Alembert               » PUISSANCE selon d'Alembert            » La notion de puissance et d'exposant dans ChronoMath

 ➔   Texte original. Seuls sont modifiés la mise en page, quelques tournures et aspects orthographiques ou grammaticaux Les mots ou les commentaires en vert sont ajoutés pour une meilleure compréhension

Ce terme a différentes acceptions selon les différents objets auxquels on le rapporte (...). On nomme exposant par rapport à une PUISSANCE, un chiffre (en caractère minuscule) qu'on place à la droite et un peu au-dessus d'une quantité, soit numérique, soit algébrique, pour désigner le nom de la puissance à laquelle on veut faire entendre qu'elle est élevée. Dans a⁴, par exemple, 4 est l'exposant qui marque que a est supposé élevé à la quartique (quatrième) puissance.  

 →  c'est dire que a⁴ = a x a x a x a et ceci correspond à la définition actuelle.

Souvent, au lieu d'un chiffre, on emploie une lettre; c'est ce qu'on appelle un exposant indéterminé : aⁿ est a élevé à une puissance quelconque désignée par n. Dans a^1/n, n désigne le nom de la racine qu'on suppose extraite de la grandeur a.  
 →  voir ci-après , →  Newton

Autrefois, pour représenter la quartique (quatrième) puissance de a, on écrivait aaaa, expression incommode, et pour l'auteur, et pour le lecteur, surtout lorsqu'il s'agissait de puissances fort élevées. Descartes vint, qui à cette répétition fastidieuse de la même racine (le nombre dont on prend la puissance) substitua la racine simple, surmontée vers la droite de ce chiffre qu'on nomme exposant, lequel annonce au premier coup d'œil combien de fois elle est censée répétée après elle-même.

»  remarquer là une petite erreur : a⁵, par exemple, n'est pas a répétée 5 fois après elle-même : nous obtiendrions aaaaaa = a⁶  →  PUISSANCE

Outre l'avantage de la brièveté et de la netteté, cette expression a encore celui de faciliter extrêmement le calcul des puissances de la même racine en le réduisant à celui de leurs exposants, lesquels pouvant d'ailleurs être pris pour les logarithmes des puissances auxquelles ils se rapportent, les font participer aux commodités du calcul logarithmique (...).

Multiplication :                

Faut-il multiplier a^m par aⁿ ? On fait la somme des deux exposants, et l'on écrit a^{m + n}. En effet que m = 3, et n = 2 :

Division :                        

Pour diviser a^m par aⁿ, on prend la différence des deux exposants, et l'on écrit a^{m - n}. En effet que m = 5, et n = 2 :

• Si n = m, l'exposant réduit devient 0, et le quotient est a⁰ = 1 car, au lieu de n, substituant m qui lui est égal par supposition :

• Si n > m, l'exposant du quotient sera négatif. Par exemple, que m = 2, et n = 5 :

a^{m - n} = a^{2 - 5} = a^-3.

• Mais qu'est-ce que a^-3 ? Pour le savoir, interrogeons l'ancienne méthode : a^-3 est donné pour l'expression de aa / aaaaa = 1/aaa = 1/a³. Ce qui fait voir qu'une puissance négative équivaut à une fraction, dont le numérateur étant l'unité, le dénominateur est cette puissance même devenue positive; comme réciproquement, une puissance positive équivaut à une fraction dont le numérateur est encore l'unité et le dénominateur cette même puissance devenue négative. En général a^-m = 1/a^m. On peut donc sans inconvénient substituer l'une de ces deux expressions à l'autre : ce qui a quelquefois son utilité.  
  →  et ceci correspond bien à la formulation actuelle.

Élévation :               

Pour élever a^m à la puissance dont l'exposant est n, on fait le produit des deux exposants et l'on écrit a^{m x n}.
En effet que m = 2, et n = 3 :

Extraction :          

Comme cette opération est le contraire de la précédente, pour extraire la racine n-ème de a^m, on voit qu'il faut diviser m par n et écrire a^m/n. En effet que m = 6, et n = 3 :

On peut donc bannir du calcul les signes radicaux qui y jettent souvent tant d'embarras, et traiter les grandeurs qu'ils affectent comme des puissances dont les exposants sont des nombres rompus (fractions) car :

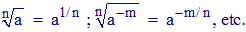
On ne dit rien de l'addition, ni de la soustraction parce que ni la somme, ni la différence de deux puissances de la même racine, ne peuvent se rappeler à un exposant commun, et qu'elles n'ont point d'expression plus simple que celle-ci, a^m + aⁿ.

(...)

Article de M. Rallier des Ourmes

Tout en qualifiant l'article "d'excellent", d'Alembert se sent obligé de compléter ... :

Il ne nous reste qu'un mot à ajouter à cet excellent article sur le calcul des exposants. Que signifie, dira-t-on, cette expression a^-m ? Quelle idée nette présente-t-elle à l'esprit ? La voici : il n'y a jamais de quantités négatives et absolues en elles-mêmes. Elles ne sont telles que relativement à des quantités positives dont on doit ou dont on peut supposer qu'elles sont retranchées. Ainsi a^-m ne désigne quelque chose de distinct que relativement à une quantité aⁿ exprimée ou sous-entendue; en ce cas a^-m marque que si on voulait multiplier aⁿ par a^-m, il faudrait retrancher de l'exposant n autant d'unités qu'il y en a dans m. Voilà pourquoi a^-m équivaut à 1/a^-m, ou à une division par a^m; a^-m n'est autre chose qu'une manière d'exprimer 1/a^-m, plus commode pour le calcul.

De même a⁰ n'indique autre chose que a^m x a^-m ou a^m/a^m = 1; a⁰ indique, suivant la notion des exposants, que la quantité a ne doit plus se trouver dans le calcul et en effet elle ne s'y trouve plus : comme a^-m indique que la quantité a doit se trouver dans le calcul avec m dimensions de moins, et qu'en général elle doit abaisser de m dimensions la quantité algébrique où elle entre par voie de multiplication. Voyez NÉGATIF.

Passons aux exposants fractionnaires. Que signifie a^1/2 ? Pour en avoir une idée nette, je suppose a = bb; donc a^1/2 est la même chose que (bb)^1/2; or dans (bb)³, par exemple, l'exposant indique que b doit être écrit un nombre de fois triple du nombre de fois qu'il est écrit dans le produit bb et comme il y est écrit deux fois bb, il s'ensuit que (bb)³ indique que b doit être écrit 6 fois; donc (bb)³ est égal à b⁶. Donc par la même raison (bb)^1/2 indique que b doit être écrit la moitié de fois de ce qu'il est écrit dans la quantité bb; donc il doit être écrit une fois; donc (bb)^1/2 = b; donc a^1/2 = b = √a.

→ Bon... mais comme disent les élèves : m'sieur vous nous embrouillez, avant j'croyais avoir compris, maintenant j'comprends plus rien...

Il n'y aura pas plus de difficulté pour les exposants radicaux dont très peu d'auteurs ont parlé. Que signifie, par exemple, a^√2 ? Pour le trouver, on remarquera que √2 n'est point un vrai nombre, mais une quantité dont on peut approcher aussi près qu'on veut, sans l'atteindre jamais; ainsi supposons que p/q exprime une fraction par laquelle on approche continuellement de √2  ; a^√2 aura pour valeur approchée la quantité a^p/q, dans laquelle p et q seront des nombres entiers qu'on pourra rendre aussi exacts qu'on voudra, jusqu'à l'exactitude absolue exclusivement. Ainsi a^√2 indique proprement la limite d'une quantité, et non une quantité réelle; c'est la limite de a élevé à un exposant fractionnaire qui approche de plus en plus de la valeur de a^√2.

»  Remarquer là un langage très moderne : c'est tout à fait l'acception d'aujourd'hui.

 Jean le Rond d'Alembert