
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

branche infinie | point asymptote | cercle asymptote | » cas y = f(x) | cas implicite f(x,y) = 0 | cas paramétré x = f(t), y = g(t) |
Le terme asymptote provient du grec asymptôtos : formé sur a (privatif) sun (avec) et piptein (tomber), soit "qui tombe avec mais sans toucher". Cette notion est connue des lycéens dès la classe de seconde avec l'étude de l'hyperbole équilatère et la mise en évidence de ses asymptotes "horizontale" et "verticale".
![]()
Notons au passage que Victor Hugo écrivit à propos de la
Science dans William Shakespeare (1864), Livre III :
«
La science est l'asymptote de la vérité. Elle approche sans cesse, et ne touche
jamais. » Pas mal, non ?... J'aime bien aussi :
«
La science cherche le mouvement perpétuel. Elle l'a trouvé : c'est elle-même.
»
Définitions (géométrie euclidienne plane) :
Un point, un cercle, une droite, et plus généralement une courbe plane (A) est dit(e) asymptote à une courbe (C) lorsque x (ou y) tend vers une limite finie ou non si la distance séparant (A) et (C) tend vers 0. Le cas le plus connu, car étudié dès la classe de seconde avec l'étude de l'hyperbole, est la droite asymptote. Voici un cas simple
➔ Dans le cas de deux courbes dont aucune n'est une droite, on dit souvent qu'elles sont asymptotes l'une de l'autre. C'est le cas, par exemple, des fonctions d'équations y = x2 (en bleu) et y = x2 - 1/x (en rouge) :

ou des sinus et cosinus hyperboliques pour x infini positif (sh x est en rouge) :

ch x - sh x = e-x. Par suite lim x →∞ (ch x - sh x) = 0 : les deux courbes sont asymptotes l'une de l'autre en + ∞.
♦ Outre le cas ci-dessous, les cas d'un point asymptote sont présentés et commentés sur les pages consacrées :
à la spirale hyperbolique (cas polaire) avec également une droite asymptote;
à la spirale logarithmique (cas polaire);
au folium de Descartes (cas implicite et paramétré) avec également une droite asymptote;
à la spirale de Cotes (cas polaire) avec également une droite asymptote;
à la spirale de Fibonacci (cas géométrique).
Cette jolie courbe paramétrée a pour équation : x(t) = (4t2 - 1)/(t3 + 1) , y(t) = (4t3- t)/(t3 + 1) , t ≠ -1. Elle admet un point asymptote de coordonnées (0,4) car si t tend vers ± ∞, alors lim x(t) = 0± et lim y(t) = 4. La courbe admet également une asymptote oblique d'équation y = 1 - x au voisinage de t = -1 :

♦ Le cas d'un cercle asymptote se présente parfois dans le cas d'une courbe définie par une équation polaire r = f(θ). Un cas est étudié sur cette page.
| Cas général pour une courbe définie par une équation cartésienne y = f(x) : |
Dans le cas général d'une courbe définie par une équation cartésienne y = f(x) :
une limite infinie pour x tendant vers une limite finie x
une limite finie pour x tendant vers l'infini (positif ou négatif) caractérise une asymptote parallèle à l'axe des abscisses (généralement qualifiée d'horizontale), d'équation y = y
o.
Les limites en ces valeurs de y = f(x) sont infinies (puisque le numérateur ne s'annule pas). Le signe est (+∞ ou -∞) est déterminé par celui du dénominateur D < 0 sur ]-2;3[, puisque le numérateur N est positif. Lorsque x tend vers ±∞, f se comporte comme ses monômes de plus haut degré*, soit comme x2/x2 = 1 : la courbe admet la droite d'équation y = 1 comme asymptote horizontale en ±∞.
(*) En classe de 1ère ou Terminale, on écrirait D = x2 - x - 6 = x2(1 - 1/x - 6/x2), donc f = N/D a même limite en ±∞ que le rapport x2/x2 = 1 car 1/x et 6/x2 tendent vers 0.
Branche infinie :
Les courbes x → sh x et x → ch x évoquées en introduction s'étendent à l'infini pour x infini. La courbe x→ x + 1/x, également évoquée en introduction s'étend à l'infini pour x infini et pour x tendant vers 0. Dans tous ces cas, on parle de branches infinies. La courbe ci-dessus admet quatre branches infinies toutes asymptotes à des droites parallèles aux axes de coordonnées.
Il n'en est pas toujours ainsi : la courbe d'équation y =
½x - 3 + 1/x admet la droite y = ½x - 3 comme asymptote non parallèle aux axes, type d'asymptote généralement qualifiée d'oblique.

Si l'on soupçonne au voisinage de infini l'existence d'une asymptote oblique y = Ax + B, une condition nécessaire évidemment que la limite de f(x) soit infinie. Si c'est le cas, par défintion d'une asymptote, la limite à l'infini (positif et/ou négatif) de f(x) - (Ax + B) est nulle. Donc f(x)/x tend vers A. D'où la démarche :
♦ on recherche A comme limite à l'infini (positif ou négatif) de f(x)/x.
• si la limite de f(x)/x n'existe pas, on parle simplement de branche infinie;
• si la limite de f(x)/x est infinie, on parle de branche parabolique de direction Oy;♦ si la limite de f(x)/x est un nombre fini A, on recherche B comme limite finie de f(x) - Ax.
• si la limite de f(x) - Ax n'existe pas, on dit que la courbe possède une branche infinie de
direction asymptotique y = Ax.
• si la limite de f(x) - Ax est infinie, on parle de branche parabolique dans la direction y = Ax
• si la limite de f(x) - Ax est un nombre B fini, la courbe admet la droite d'équation y = Ax + B
au voisinage de l'infini considéré.
➔ Pour une fonction rationnelle irréductible en x, f(x) = P(x)/Q(x), lorsque P est de degré n et Q de degré n - 1, la méthode de division polynomiale, due à William Horner permet d'exhiber l'équation de l'asymptote oblique. Exemple :


Dans ce cas, la division euclidienne de x3 + 2x2 - x - 2 par x2 + 1 fournit :
![]()
faisant apparaître l'asymptote oblique y = x + 2 pour x infini.
En savoir plus : »
| Droite asymptote dans le cas d'une équation paramétrique x = f(t), y = g(t) : |
Ce cas se traite de manière semblable au cas cartésien y = f(x) : si, au voisinage d'une valeur to du paramètre t, x = f(t) et y = g(t) admettent des limites infinies, on calcule la limite en t
o de y/x = g(t)/f(t) afin de déterminer une direction asymptotique. Il s'agit donc de la recherche du coefficient directeur A d'une asymptote éventuelle. Si A existe et est fini, on calcule la limite de y - Ax. Les conclusions sont les mêmes.Exemple :
La courbe paramétrée ci-dessous a pour équation : x(t) = (4t2 - 1)/(t3 + 1) , y(t) = (4t3- t)/(t3 + 1) , t ≠ -1. Lorsque t tend vers -1 x et y tendent vers l'infini. Ces branches infinies admettent-elles une (ou des) asymptote(s) ? On remarque que y = tx; donc y/x = t tend vers -1. Calculons maintenant la limite de y + x. Au numérateur nous avons (4t3- t + 4t2 - 1) = (t + 1)(4t2 - 1). Au dénominateur : t3 + 1 = (t + 1)(t2 - t + 1). En simplifiant pat t + 1 et passage à la limite, on constate que y + x tend vers 3/3 = 1 : la courbe admet l'asymptote "oblique" d'équation y = 1 - x. Noter que cette jolie courbe admet également un point asymptote de coordonnées (0,4) pour t infini.

| Droite asymptote dans le cas d'une équation implicite f(x,y) = 0 : |
Ce cas est très spécifique, suivre le lien ci-dessous :
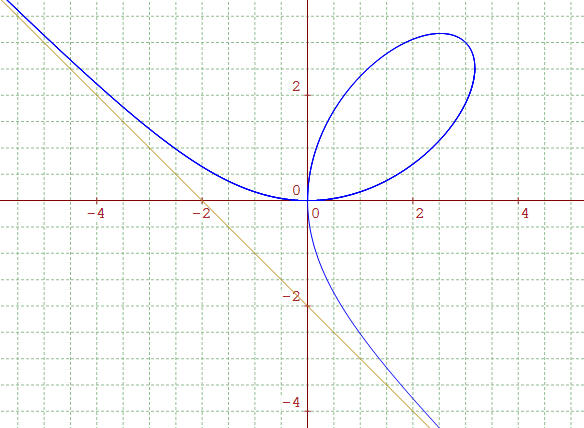
cas du folium de Descartes x3 + y3
= 3kxy; ci-dessus k = 2, asymptote oblique y = -x -2
Asymptotes à une courbe algébrique définie par une équation implicite f(x,y) = 0 : »
| Droite asymptote dans le cas d'une équation polaire r = f(t) : |
Cas encore plus spécifique, il est étudié sur les pages consacrées :
à la spirale hyperbolique (cas polaire); à la spirale de Cotes (cas polaire);
au folium de Descartes (cas implicite et paramétré);