ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Comportement à l'infini  de f(x) = 2(16 + x2)½ - x         » cas plus dur...

On pose :

1°. Justifier brièvement que f est continue et dérivable sur R tout entier et que sa fonction dérivée f ' est du signe de :

2°. Résoudre l'inéquation : x∈R, f '(x) ≥ 0        Rép. : x ≥ 4/√3

3°. Justifier que l'on peut écrire pour tout x non nul :

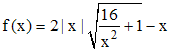
En déduire que la courbe (c) représentative de f dans un repère orthogonal admet deux asymptotes obliques d'équations respectives :

y = x  et  y = -3x