ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Trisectrice
de Maclaurin |
Dans le cadre de la
célèbre trisection
de l'angle initiée par Hippias, le mathématicien écossais
Colin MacLaurin présenta une courbe permettant la construction approchée du tiers d'un
angle donné.
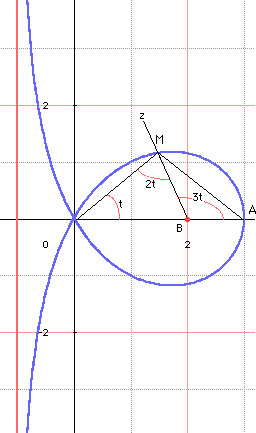
Dans un repère orthonormé (Ox,Oy), considérons un point A(3a,0) et le point B(2a,0). Soit M un point du plan tel que dans le triangle AOM nous ayons ^AOM = t et ^ABM = 3t. L'angle ^AOM réalise alors, par définition du problème, la trisection d'un angle ^ABz donné.
Étudions, en coordonnées polaires, l'ensemble des points M(t,r) permettant cette trisection :
➔ Rappelons que dans tout triangle ABC, de côtés a = BC, b = AC, c = AB, on a la relation :
a/sin(^A) = b/sin(^B) = c/sin(^C) = 2R
où R désigne le centre du cercle circonscrit.
Par suite, dans le triangle OMB, on a la relation :
2a/sin(^OMB) = r/sin(π - 3t)
Or, dans ce triangle : ^OMB = π - t - (π - 3t) = 2t
L'équation polaire de la courbe décrite par M est ainsi :
Une transformation élémentaire sur sin3t = sin2t.cost + sint.cos2t conduit à une autre forme :
Conclusion : on peut aussi placer l'origine des coordonnées en B(2a,0) et considérer le point M(r',t') avec t = t'/3. Ce n'est là qu'une approximation d'une trisection puisqu'elle est n'est pas une construction au sens d'Euclide à la règle et au compas !
Remarque : l'application de la formule de Pythagore généralisée permet d'écrire r'2 = r2 + 4a2 - 4ar.cost, ce qui fournit très facilement :
r' = a/cost = a/cos(t/3)
C'est sous cette forme que Gohierre de Longchamps étudia la rectification de cette courbe qui s'avère donc être un cas d'épispirale.
Comme la strophoïde, qui lui ressemble, la trisectrice de Maclaurin est une cubique. Elle est analllagmatique. Son équation cartésienne s'obtient facilement en remarquant que sin 3t = 3sin t - 4sin3t et sin 2t = 2sint.cos t. Ainsi r peut s'écrire :
et vu que x = r.cost, y = r.sin t et r2 = x2 + y2, on a ici :
Trisection : selon Archimède : » selon Céva : » selon de Lonchamps : »