ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Développante
d'une courbe
» application
: à la chaînette
, au cercle , à la cycloïde |
Cette notion fut initiée par Huygens. Considérons une courbe Γ comme ci-dessous en rouge et A un point de Γ (ici le point d'intersection de Γ avec l'axe des ordonnées).
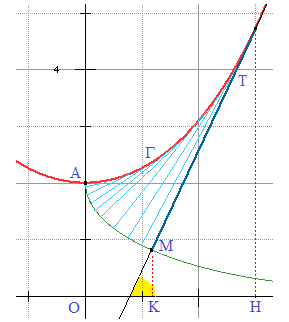
Supposons qu'un fil ait été plaqué le long de la courbe depuis A, sur la portion correspondant à x positif, et que nous cherchions à décoller ce fil en le conservant tendu et tangent à Γ.
Les étapes sont en bleu sur le graphique ci-contre. L'ensemble des extrémités M décrit une courbe appelée développante de Γ par rapport à A. Supposons que la courbe Γ soit paramétrée :
T(x,y) ∈Γ ⇔ x = x(t) , y = y(t)
T se projette en H sur l'axe des abscisses; M se projette en K. On suppose que sur l'intervalle d'étude, x et y admettent, au moins, des dérivées première et seconde continues.
En considérant deux valeurs infiniment proches du paramètre t et t + dt, si l'on trace les perpendiculaires en M(t) et M(t + dt) aux tangentes (TM), lorsque dt tend vers 0, le point M apparaît comme point de contact de la développante avec son cercle de courbure centré en T.
C'est dire que la courbe (Γ) n'est autre que le lieu des centres de courbure de sa développante, donc la développée de sa (ses) développante(s).
On peut aussi dire qu'une développante de (Γ) est une trajectoire orthogonale des tangentes à (Γ) : "chemin" coupant perpendiculairement toutes ses tangentes. Le cas général des trajectoires orthogonales à une famille de courbes a été étudier par Stirling (et Fontaine) en réponse à un défi lancé par Jean Bernoulli.
Détermination des trajectoires orthogonales à une famille de courbes : »
| Étude : |
Si s désigne la longueur de l'arc de courbe AT, on a s = MT et en notant û l'angle que fait la tangente (MT) avec l'axe des abscisses, on a, en mesure algébrique :
HK = MT × cos û = s × cos û, û = ^(Ox,MT)
où s désigne la longueur de l'arc de courbe AT.
x' et y' désignant les dérivées de x et y par rapport à t, posons pour simplifier n2 = x'2 + y'2.
On a n > 0 en tout point régulier et tan û = y'/x'. Par suite :
cos û = εx'/n avec ε = ±1
En notant M(X,Y), on a :
La mesure de û varie entre 0 et π. Lorsque û est obtus , on a HK > 0 (ε = -1), sinon HK < 0 (ε = +1). D'où :
X = x - s|cos û| = x - sx'/n
Un calcul analogue conduit à Y. D'où l'équation de la développante par rapport à un point A :
∗∗∗
Cas de la chaînette,
proposé en exercice corrigé :
L'équation cartésienne de la
chaînette est : y = acosh(x/a). Pour
simplifier les calculs, on prendra a = 1.
Montrer, en utilisant les résultats
précédents, que l'équation de la
développante est alors :
X = ln | tan(û/2) | + cosû , Y = sin û ☼
Chaînette (en bleu) - Développante (en rouge)
Tractrice : »