ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 

Méthode des différences finies          » programme JavaScript      Méthode d'Euler pour la résolution approchée d'une équation différentielle

La résolution d'une équation différentielle

x∈J, Φ(x,y,y',y",...) = 0, y = f(x)

par différences finies consiste à discrétiser l'intervalle d'étude J = [a,b] sur lequel est définie l'équation. On recherche une solution approchée sous la forme d'un nuage de points (x_i, y_i), y_i = f(x_i). Les x_i sont connus, les y_i sont l'objet de la recherche.

Considérons le cas d'une équation différentielle du 1er ordre, se ramenant à la forme simple :

y' = φ(x,y), avec x_o , y_o donnés           » problème de Cauchy

On sait qu'une approximation de y' = f'(x) est donnée, pour h "petit", par le quotient des différences finies Δy/Δx (taux d'accroissement) :

Comme dans le cas de l'intégration approchée, subdivisons J en n sous-intervalles (de même amplitude pour simplifier l'algorithme) :

a = x_o  < x₁ < x₂ < ... < x_n= b , x_i = a + ih, h = (b - a)/n

Si y_n désigne l'approximation de f(x_n), on peut écrire alors écrire :

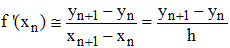
Notre équation différentielle y' =  φ(x,y) s'écrit alors :

y_n+1 - y_n = hφ(x_n,y_n),   x_o, y_o donnés

en espérant que le processus est convergent, ce qui est le cas lorsque f est suffisamment lisse : au moins de C¹ (continue ainsi que sa dérivée première) sur l'intervalle J. Cependant, la précision est d'ordre 1 (en 1/h). Ce qui est faible. Pour des équations non pathologiques (évitez d'intégrer au voisinage d'une asymptote de la courbe intégrale...), il y a peu d'espoir d'un résultat satisfaisant si h > 1/1000 : évitez d'intégrer sur des intervalles de forte amplitude.

Pour une étude rigoureuse de la méthode (consistance, choix judicieux de h, convergence, erreur commise), on pourra se reporter aux références indiquées in fine et tout particulièrement à l'excellent livre de Claude Brezinski (professeur honoraire de l'université des sciences et techniques de Lille) : Algorithmique numérique (» réf.4): on ne peut que très difficilement faire mieux à ce sujet.

La représentation graphique du nuage de points M(x_i, y_i) obtenus fournit une approximation de la courbe intégrale dont on peut ensuite rechercher une équation approchée (polynomiale, logarithmique, exponentielle) par diverses méthodes d'approximation polynomiale ou non, comme par les moindres carrés, fournissant une expression acceptable de f.

Approximation et polynômes orthogonaux : »

Pour une fonction ne posant pas de problème aux bornes de J, il peut être plus judicieux d'utiliser la dérivée symétrique :

conduisant à :

L'algorithme se programme très facilement. On peut bien entendu l'améliorer pour contrôler la convergence et évaluer l'erreur commise.

 ➔    Pour tester ce programme vous devez entrer votre fonction φ(x,y) en utilisant une syntaxe comprise par le langage JavaScript. L'instruction with (Math), placée en début de procédure, évite à l'utilisateur de préciser Math devant chaque fonction mathématique utilisée. Les opérations et fonctions usuelles sont les suivantes :

• multiplication : * ,   division : /
• racine carrée : sqrt(x)
• puissance : pow(x,n). Pour x² ou x³, utiliser plutôt x*x et x*x*x
• fonctions usuelles : sin(), cos(), tan(), atan(), abs();
• log népérien : log() , exponentielle de base e : exp() , ...
• les appellations pi (pour π) et e sont comprises par le programme.

Le programme utilise par défaut l'équation différentielle  y' + y + 1 = e^x  sur [0,1] avec y(0) = 1/2. On entre y' = φ(x,y) sous la forme exp(x) - y - 1.  J = [0,1], x_o = 0, y_o = 1/2. La solution exacte est : y = e^-x + ½e^x - 1