ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Perspective axonométrique oblique, dite perspective cavalière

La représentation d'un objet en perspective cavalière, couramment utilisée dans l'étude de la géométrie de l'espace au collège et au lycée car simple dans sa mise en œuvre (également appelée perspective parallèle car elle respecte le parallélisme), n'est pas conforme à notre vision du monde, donc non conforme à ce qu'attend notre cerveau, à savoir la réduction des dimensions avec l'éloignement.

Face à deux droites parallèles fuyant vers l'horizon, on devrait faire apparaître un rétrécissement tel une route rectiligne ou des rails observées dans une gare ou du haut d'un pont.

La véritable perspective (du latin perspicere = voir à travers) est la perspective conique (également dite centrale) : le dessin que reproduirait le peintre en suivant les contours d'un objet de l'espace observé à travers une vitre.

Perspective centrale : »

Traversée du Chott El Jerid en direction de Tozeur (sud tunisien)

La perspective axonométrique (du grec axon = axe et metron = mesure) est un cas très particulier de perspective centrale, l'œil O de l'observateur (figure ci-dessus) étant considéré à  l'infini et les "rayons" (comme OM) sont parallèles (comme ceux du Soleil). Si le plan de projection (la vitre servant de feuille à dessin) est orthogonale aux rayons, on parle d'axonométrie orthogonale. Dans le cas contraire on parle d'axonométrie oblique également appelée perspective cavalière.

 ➔  La perspective cavalière est une représentation plane de l'espace tenant son nom des architectes militaires (et non d'un cavalier au sens d'un homme à cheval ou de Cavalieri !) : en termes de fortifications, un cavalier est (était) une butte intérieur à un fortin, dominant par rapport aux constructions qui l'entourent et permettant aux soldats de garde de surveiller les environs :

       
Illustrations extraites du Nouveau Larousse Illustré (1904). L'une en perspective cavalière, l'autre en coupe dite XY.

Le plan de projection est a priori oblique relativement à chacune des trois directions des axes d'un repère R = (O,x,y,z) de l'espace. Le repère de la feuille à dessin est alors la projection R' = (O',x',y',z') du repère R fixant ainsi, en considérant les projections des points unités, les rapports de distances, suivant les trois directions, entre l'image réelle 3D et sa projection.

En convenant d'observer la feuille de sorte que la projection (O'z') de (Oz) soit représenté "verticalement", les projections des axes (O'x') et (O'y') font alors sur le dessin des angles a et b avec "l'horizontale".

La perspective cavalière correspond au cas particulièrement simple b = 0 et à un même rapport en y' et z'. Si a = b, on parle de perspective isométrique, dont il y a lieu de se méfier... : la figure ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
a = b = 30°. Voyez-vous un hexagone régulier du plan ou un cube de l'espace ? Déplacer la demi-droite (Oy)...

Concrètement la perspective cavalière se traduit par des figures non déformées si elles sont vues de "face" : figures de l'espace appartenant à des plans parallèles au plan (y'O'z'). La perspective d'un carré est alors un carré, celle d'un cercle est un cercle, etc.

La profondeur est rendue en utilisant généralement un coefficient de réduction généralement entre 0,5 et 0,7) et un angle a entre 30 et 45°. Ces choix sont purement subjectifs et dépendent tant du dessinateur que de l'objet à représenter, l'objectif étant un dessin réaliste.

Voici une maison en perspective :

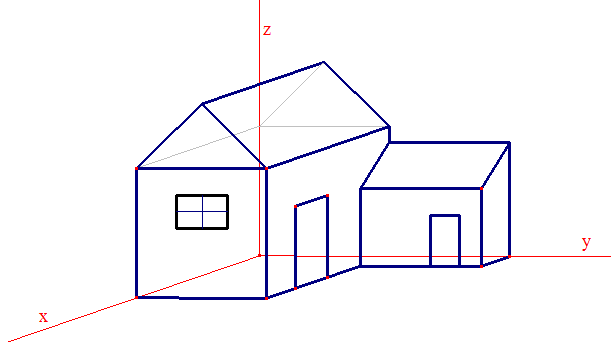
Si votre navigateur accepte les applets Java (» extension CheerpJ) :
En déplaçant (Ox), en augmentant a, on semble passer à gauche de la maison.
Vérifiez cet effet en déplaçant le demi axe (Oy) ou (Ox).

 ➔  Un angle b non nul apportera une impression de plus grande proximité vers la droite par rapport à un observateur (virtuel) : en le faisant varier, dans un dessin animé ou un jeu vidéo, on pourra suggérer, image par image, une approche ou un recul par rapport à l'objet dessiné.

La perspective cavalière, en tant que projection parallèle, particulière, conserve :       

• le parallélisme;

• l'alignement;
• les milieux;
• les rapports de distances sur des segments parallèles.

 !  La perspective cavalière ne conserve pas les angles des figures qui ne sont pas vues de face : elle a tendance à les écraser... Un rectangle ou un carré devient un parallélogramme, un cercle devient une ellipse, une sphère devient un ellipsoïde. Pire, un angle de 100° peut apparaître droit en perspective !

Au collège et au lycée, pour éviter des confusions d'interprétation dues à ces déformations, il est souhaitable de coder la figure (angles et segments) et de tracer en pointillés les arêtes qui seraient invisibles si l'objet était opaque.

A gauche, la face supérieure du prisme semble isocèle. A droite, on a le même prisme en "transparent" et on a codé deux angles comme étant droits : un cerveau (normalement constitué...) conviendra de cette rectitude et admettra sans rechigner l'inégalité BC > BA !

 ➔  Pour en savoir plus :

• La perspective par Albert Flocon et René Taton, Que sais-je ? n°1050, Éd. Presses Universitaires de France - 1963, rééd. 1994.

• On pourra consulter un important chapitre sur les différents types de perspective dans :
  Histoires de problèmes. Histoire des Mathématiques, Commission Inter-I.R.E.M. , Éd. Ellipses - 1993.