
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
Rappelons que si f une fonction continue et positive sur un intervalle [a,b], la méthode des trapèzes pour le calcul de l'intégrale :
![]()
consiste à remplacer l'arc de courbe MiMi+1 par le segment [MiMi+1].

Si nous choisissons une subdivision régulière de l'intervalle [a,b] en n sous-intervalles [xi,xi+1] avec i variant de o à n :
en posant h = xi+1 - xi = (b - a)/n, on a xi = a + ih et le nombre J(h) ci-dessous est une approximation de I :

l'erreur commise étant en 1/n2.
|
Où l'on retrouve la méthode de Simpson par extrapolation : |
La méthode des trapèzes consiste en une interpolation linéaire (chaque arc de courbe est remplacé par un segment). Montrons comment, par un artifice de calcul, on peut obtenir une erreur en 1/n4 et retrouver la méthode de Simpson qui est une interpolation parabolique (chaque arc de courbe est remplacé par un arc de parabole) :
On se place dans le cas d'une fonction f indéfiniment dérivable. L'erreur ei(h) sur [xi, xi+1] = [xi,xi + h] est, selon la formule de l'aire d'un trapèze :
et selon la formule d'Euler-Maclaurin, on peut écrire ei(h) sous la forme, a2 et a4 étant des constantes :

En notant e l'erreur commise sur l'intervalle [a,b] d'intégration, on peut écrire alors, par sommation, α et β étant des constantes :
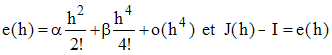
Doublons le nombre de points :

En théorie, J(h/2) apparaît 4 fois meilleure. Multiplions par 4 :
![]()
Soustrayons membre à membre J(h) - I = e(h) à cette dernière égalité et divisons par 3 :
 (ex)
(ex)
Le premier membre est une extrapolation obtenue à partir de J(h) et J(h/2). C'est une approximation de I avec une erreur en h4, donc en 1/n4 au lieu de 1/n2 : il s'agit bien là d'une accélération de convergence.
Considérons alors la formule des trapèzes pour n = 1 : xo = a < x1 = b. On a alors :
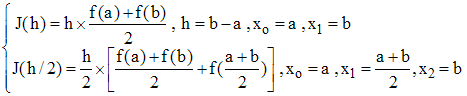
L'approximation extrapolée est alors :

Il s'agit de l'approximation de I par la méthode de Simpson réduite à 3 points (n = 2).
| Extrapolation de Richardson, Formule récurrente de Romberg : |
Généralisons le résultat (ex) précédent. On peut itérer la méthode afin d'obtenir une nouvelle extrapolation. Selon la formule d'Euler-Maclaurin, le développement limité de l'erreur commise ne contient que des puissances paires de h. Supposons alors avoir obtenu une approximation J(h) de I avec une erreur en h2k.
On a :
D'où :
Posons :
 (ex2)
(ex2)
Le terme en h2k dans le développement de I a disparu : en choisissant K(h) comme approximation de I, l'erreur est en h2k+2.
➔ Cette méthode de calcul est appelée extrapolation de Richardson. Elle peut s'appliquer à tout algorithme de calcul d'un nombre réel R lorsque celui-ci est approché par une fonction R(h) avec une erreur e(h) admettant un développement limité :
R =R(h) + e(h) avec e(h) = ahk + bhk+1 + c hk+2 + ... et lim h→o e(h) = 0.
Afin de faire apparaître une relation de récurrence entre les extrapolations successives, changeons nos notations :
J(h) dépend de h = qui est une fonction du nombre d'intervalles de la subdivision. Forçons ce nombre à être une puissance de 2, soit 2n : la formule des trapèzes pour trapèzes pour xo = a < x1 = b, avec h = b - a, correspond maintenant à n = 0 (20 = 1).
Notons désormais R(n,0) les précédents nombres J(h) résultats de la méthode des trapèzes.
Les extrapolations obtenues en ex2 à partir des J(h) et J(h/2) pour h = (b - a)/2n sont les premières itérations que nous notons R(n,1)
Nous pouvons désormais, sans plus appliquer la méthode des trapèzes, accélérer la convergence au seul moyen des R(i,j) issus de l'extrapolation de Richardson. En effet, considérons R(1,1) et R(2,1) calculés en ex2 : ils sont de la forme R(1,1) = I + ah4 + o(h4) et R(2,1) = I + a(h/2)4 + o(h4) et on peut leur appliquer l'extrapolation de Richardson afin d'obtenir un R(2,2) avec une erreur théoriquement en h6.
Faisant de même avec R(2,1) et R(3,1) on obtient un R(3,2) avec une erreur en h6 et l'extrapolation entre R(2,2) et R(3,2) fournira un R(3,3) avec une erreur théoriquement en h8. Et ainsi de suite.
! Il faut bien dire théoriquement en parlant de l'erreur car il se greffe pour des valeurs petites de h des erreurs d'arrondi difficilement contournables dont les effets peuvent être dévastateurs. Dans Chronomath, on pourra consulter les pages : accumulation des erreurs d'arrondi, ordinateur et arrondis, système binaire et arrondis.
| R(0,0) | R(1,0) | R(2,0) | R(3,0) | R(4,0) | ... | R(n-1,0) | R(n,0) |
| R(1,1) | R(2,1) | R(3,1) | R(4,1) | ... | R(n-1,1) | R(n,1) | |
| R(2,2) | R(3,2) | R(4,2) | ... | ... | ... | ||
| R(3,3) | R(4,3) | ... | ... | ... | |||
| R(4,4) | ... | R(n-1,k-1) | R(n,k-1) | ||||
| ... | R(n,k) |
Le tableau ci-dessus résume les extrapolations successives. On a la formule de récurrence (attention aux indices !) :

où R(n,0) représente l'approximation par la méthode des trapèzes pour le pas h = (b - a)/2n.
| Programmation de la méthode en JavaScript : |
Le programme exploite la récurrence étudiée et possède un double test de fin : précision atteinte et n > 100 afin d'éviter une boucle infinie en cas de non convergence : cas d'une fonction "trop irrégulière", car n'oublions pas que nous avons supposé f indéfiniment dérivable !
➔ Pour tester ce programme vous devez entrer la fonction f utilisée en utilisant une syntaxe comprise par le langage JavaScript. Cependant, l'instruction with (Math), placée en début de procédure, évite à l'utilisateur de préciser Math devant chaque fonction mathématique utilisée.
multiplication : * , division : /
racine carrée : sqrt(x)
puissance : pow(x,n). Pour x2 ou x3, utiliser plutôt x*x et x*x*x
fonctions usuelles : sin(), cos(), tan(), atan(), acos(), asin(), abs(); log népérien : log() , exponentielle de base e : exp() , ...
les appellations pi (pour π) et e sont comprises par le programme.
» fonctions mathématiques usuelles
Par défaut f(x) = 1/x. C'est dire que nous calculons des approximations du logarithme népérien de x en donnant à la borne inférieure a la valeur 1 et en donnant à b une valeur strictement positive de notre choix.
Pour une fonction assez "régulière", le programme est très performant. On peut obtenir jusqu'à 8 décimales exactes : entrez ce nombre noté p (précision). Le nombre de subdivisions est 2, 4, ..., 2n. On vous demandera de donner n.
Le programme s'arrête dès que |r(i,j) - r(i-1,j)| < 10-p. Si l'algorithme diverge (test non vérifié), le programme vous avertira (diminuez p ou augmentez prudemment la valeur de n.
! Évitez un trop grand nombre de points pouvant créer des erreurs d'arrondi engendrées par un pas (b - a)/2n trop petit !
|
Un exemple d'application : |
On a tracé ci-dessous la courbe d'équation :

admettant y = x+2 comme asymptote oblique. L'aire coloriée en jaune est I, intégrale de -2 à +2 de la fonction g(x) = x + 2 - f(x).
En entrant la fonction :
x+2-(x*x*x+2*x*x-x-2)/(x*x+1) ,
la méthode de Romberg fournit avec les paramètres par défaut : I = 8,8571897325... En demandant 8 décimales, l'algorithme converge en fournissant : I = 8,85718974174...≅ 8,857189742 : excellent résultat.

Comparaison à la valeur exacte :
Par division, on obtient f(x) = x + 2 - (2x+4)/(x2 + 1). Par suite g(x) = x + 2 - f(x) = (2x+4)/(x2 + 1) = 2x/(x2 + 1) + 4/(x2 + 1). Une primitive de g est donc ln(x2 + 1) + 4Atn(x). L'aire cherchée est alors 8Atan(2) ≅ 8,857189742.
Méthode de Milne (autre application de l'extrapolation de Richardson) : » Autres méthodes : »